[現在の伯母野山日記の一番最近の記事]
[2011年以前の伯母野山日記の記事]
[2012年から2016年の間の伯母野山日記の記事]
[春日井日記]
[バルセロナ日記]
[バルセロナ日記 (2008年4月20日以前の日記)]
[もどる]
※ この page の内容(html file のコードを含む)の GNU Free Documentation License に準拠した引用/利用は歓迎しますが, 盗作/データ改竄やそれに類する行為には 天罰が下ります. 絶対にやめてください. ただし,ここで書いたことの一部は, 後で,本や雑誌記事などとして発表する作文の素材として再利用する可能性もあります. その際,再利用されたテキストに関しては, 諸事情から GNU Free Documentation License に準拠した扱いができなくなることもありますので, その場合にはご諒承ください.
※ 私は夜型人間なので (学生の頃に,やはり夜更かしの傾向の強い下宿のおばさんに深夜に家の廊下でばったり会って ,,Sie sind ja auch Nachteule!“ と言われたことがありました), 以下で用いられているタイムスタンプでは,日付変更は深夜の4時に行なっています.たとえば, 11.07.22(金02:35(JST)) は通常の時間表示では日本時間の 2011年 7月23日(土) 2時35分です.
[少し (つまり,かなり) 前の記事] :
Tree as a metaphor of the universe
角田 譲先生を偲んで
Vierfacher Salchow
シンガポールと日本語
完全性定理と私
聖坂は慶應三田キャンパスのそばにある坂道で, 西脇順三郎の詩に出てくることで不滅のものとなった地名である.
ちなみに, 西脇順三郎の『六月の朝』という詩の最初に出てくる, 「ひじり坂と反対な山に//暗い庭が一つ残つている」と歌われている「暗い庭」は,現在 「慶應三田キャンパス」と呼ばれている慶応大学の敷地であろう.
高木貞治が彼の随想で引用している Professorenwitze は Hilbert に対して, ということでは敬意を込めた笑いなのでしょうが, 高木貞治が当時ヒルベルトの周りで画期的な進展をとげていた数理論理学や,ヒルベルトの 「数学の基礎付け」を, その数学的細部だけでなく,その意義についても明らかに理解できないでいたことから, 彼の書いたこの随想は, 「ヒルベルトは歳をとって耄碌して数学の基礎付けのようなあやしげな研究に手をそめている」 というようにも読めるような表明の含まれている, ちょっと痛い作文と言えなくもないものになってしまっています.
absent-minded professor (これはドイツ語では „zerstreuter Professor“ です. フランス語にも «professeur distrait» という表現があるようです) のジョークは, 研究に集中した結果日常生活で普通の人のやらないヘマをやらかしてしまう, というパターンのジョークなわけですが, これは,「普通の学校の先生」であることを義務づけられていることの多い日本の教授には, あまり適用できない概念かもしれません.
いずれにしても,この種類のジョークは,日本では, 一般の人が, この「研究に集中した結果」というところを全く理解できずに誤解してしまう恐れがあるので, 研究者のコミュニティーの外ではあまり話さない方がいい種類のジョークなのかもしれせん.
The reaction of the Japanese audience to the “Sannomiya Incident” he mentioned in his speech was quite interesting. He also wrote down this story in his webpage.
As I already mentioned it here the pattern of the story telling Joel took in his speech was apparently quite unknown for people in Japan (at least unknown for them in connection with a banquet speech), I suspect that many Japanese among the audience could not follow Joel's story.
Actually right after the banquet, one of Japanese students asked me how much of the story Hamkins-san told was real.
Of course every thing in the story was (super-, sur- etc.(if you will)) real just by being detatched from the “realism”.
でも他の階を見なかったことで, 後で,Cellini の塩壺が展示品の中あって,これを見逃してしまっていたことに気がついた. この塩壺は西脇順三郎の 『第三の神話』に収録されている『神話』の最後で言及されている.
...
チェリーニーの作つた舟の形をした
塩壺などはあまりに人間的だ
あまりに悲劇的な哲学なものだ
テルスという土の女神とネプチューンと
いう海の男神とが
足をからめて向きあつて
身をそらして
人間の旅の果てを示すのだ
テルスの舌に触れる時
あたゝかい土の悲しさがわかる
The lines by Junzabro Nishiwaki above look like a prose simply describing the Saliera of Cellini, and a simple machine translation would produce such an uninteresting description. I tried to produce something corresponding more closely to the original lines which ends the poem 『神話』included in the collection of the poems 『第三の神話』(1956, The title of the poem suggests that this is the main poem in the collection) in a conversation with ChatGPT.
The saltcellar, shaped like a boat,
wrought by Cellini’s hand—
is all too human.
All too steeped in tragic philosophy.
Tellus, the earth-goddess,
and Neptune, god of the sea,
entwine their legs,
face each other,
arch their bodies away—
a sign of where the human journey ends.
The warm sorrow of the soil is felt
touching the tongue of Tellus
The very last change is done by me without consulting ChatGPT.
* * *
$\mathcal{P}$-LgLCA for LC (Laver-generic Large Cardinal Axiom for given class $\mathcal{P}$ of posets and notion LC of large cardinal) is the assertion that $\kappa_{\mathfrak{refl}}:=\max\{\aleph_2,2^{\aleph_0}\}$ is the critical point of $\mathcal{P}$-generic elementary embeddings which are established "resurrectingly", whose target models are closed with respect to the closure property of LC, and the target models know well about the generic extension involved.
I shall discuss some topics in connection with this family of axioms, and open problems in their context.
子供のときに単なる偶然で手した,文学の香りを持った最初の本の一つにすぎない, とも言えるのだが,HAL の最後のユニットモジュールがはずされる瞬間のような時が来たときに, 僕はこの本のことを思い出しているかもしれない.
ただし,そのような和が有限の数として定義される (well-defined になる) のは, 和に現れる実数が,可算個を除くとすべて $0$ になるときしかありえません (たとえば, 上の例で言った非可算個の互いに素な可測集合の族の, それぞれの集合の測度からなる非可算数列では自動的にこれが起っています — これらのことの証明は読者の演習とします).
でも,数列の無限和はきちんと定義されずに教えられていることが多いように思えます. 長さが $\omega$ の普通の無限数列ですらそうなので, それを越えた transfinite な長さの数列や添字集合が必ずしも整列されていない数列の和の定義は殆どどこにも書いていない, というのが実際のところなのではないでしょうか,
撲の知っているもので,この定義がクリーンに述べられているソースの一つは,Jech の green book (Set Theory 1978) の 229ページです.この本は,「実数の集合論」の前夜に書かれているので, 当然 Tomek Bartoszyński の名前も Jacek Cichoń の名前も出てきません. むしろこの教科書のこのページ前後に書いてあることは, この二人を実数の集合論の研究へと後押しするきっかけになっていたかもしれません. Tomek にはもうじき会うことになっているので,ちょっとこの歴史の証人というか当事者本人に, このことについて確認してみたいような気がします.
最大の奇蹟は
奇蹟が起らないことだ
天使が出てこないことも
おどろくべきそれだ
水の上を歩けないことも
おどろくべきことだ
ウグイスが
薮をつき通した
キラット!
---- 西脇順三郎 『奇蹟』,鹿門 (1970)
天使が出てこないことで,天使が出てくることが暗示され, 水の上を歩けないことで,水の上を歩くキリストや聖人たちが暗示される. ウグイスの鳴き声が薮をつき通すという本当の奇蹟 (でない奇蹟) は,ボルネオ語の kilat (稲妻) のことかもしれないオノマトペーに集約されて,詩の最終行という奇蹟になっている.
海の崖の上で農夫が畑を耕している
るり草のような海が下に見える
よく見ると帆船の近くに
イカルスの足が見える
いまイカルスが落ちたばかりだ
イカルスの失墜が人が注意しない
どこかのすみで行われている
---- 西脇順三郎 『人間の没落について』, 第三の神話 (1956)
この最後の 『第三の神話』からの引用は, もちろんブリューゲルのイカルスの失墜の絵を頭に置いて書いているものだと思いますが,それを
イカルスの失墜が人が注意しない
どこかのすみで行われている
と説明することで,絵から読み取れる, causality ちぐはぐさを, 西脇順三郎の強調した「遠いものの連結」とも,他の2つの引用にあるような, 「奇蹟」でない「奇蹟」という考え方にも結びつけているわけです.
彼が手厳しく批判している本は日本語にも訳されているようなので, これは日本の読者への注意にもなるだろう.前から,私が言わなければならないかもしれない,と思っていたことを Moore が全部言ってくれているので,大変に助かる.
私は,昔,Moore がこの書評で,書評のもともとの対象にはなっていないけれど, ほとんど手放しで推薦している本の,とても問題のある日本語訳について,ネット上で批判 [2] をしたことがあった. 私はこれらの本とは別の,日本語の著者によるゲーデル本の書評をここ [3] でしたこともある.
脚注
[1] The Incomplete Gödel
[2] バルセロナ日記: G
の伝記の翻訳 [K] について
[3] [[[不完全性定理に挑む]に挑む]に挑む],
ゲーデル(著), 林晋, 八杉満利子(解説、
翻訳), ゲーデル 不完全性定理
$\pi$ が normal number であることは広く信じられているが,これが十進法について normal number であることもまだ証明されていない.normal numbers の全体は $\mathbb{R}$ の co-null subset になるので, $\pi$ がその要素になっていてもおかしくはないようには思える.$\pi$ が normal number であることは $\pi$ のどの $n$ に対する $n$進法表示も, 有限長のランダムネスをコードするものになっているということである,と解釈することができるだろう.
集合論で最近導入された,CCA (Continuum Coding Axiom) という公理がある. これは, 一般連続体仮説の成り立っているような非極限基数の,基数の区間での分布パターンが, すべての集合をクラス回の重複を伴ってコードしていることを主張する公理である. 「非極限基数」となっているのは, 特異基数の極限基数での基数の羃は,その下での基数の羃に影響されることが分っている (例えば Silver の定理は,そのような現象についての古典的な結果である) からである.
この公理は,任意のトリヴィアルでない,集合による強制拡大で,壊れてしまう,という大変に脆弱なものだが, この公理が成り立っていると,それから Ground Axiom と呼ばれる, 集合論のユニヴァースがトリヴィアルでない内部モデルの強制拡大になっていないことを主張する公理を導く (もちろん Ground Axiom も,トリヴィアルでない,任意の集合による強制拡大で崩れる).
この公理は,巨大基数公理や,巨大基数公理から出発して強制できることの知られている公理たちとは 共存不可能なのではないのか,と思えるかもしれないが, クラス個の超コンパクト基数の存在と無矛盾であることは, この公理のモデルのクラス強制による構成からすぐに分かるし, 実はそれに $\mathsf{MM}^{++}$ を加えても無矛盾である (後者については,[1] の Theorem 6.3 の証明で触れている).
この公理を``正しい''公理と看倣すべきかどうかは,よく分らないような気もするのだが, この公理の 「$\pi$ は normal number である」 という主張とのアイデアの類似性には注目してよいように思える.
[1] Sakaé Fuchino, Takehiko Gappo, and Francesco Parente, Generic Absoluteness Revisited, submitted.
日本側の企画に 「ウーマンズ パビリオン」というのがあるが, こういう名前のパビリオンを作ると世界の笑いものになる (かどうかはちょっと微妙かもしれないが,少なくともヨーロッパでは笑いものになるだろう), という感覚のないおやじたちが日本側の企画の決定権をにぎっていることがよく分かる.
入ってみたパビリオンで最悪だったのはドイツだったが, インドネシアとポーランドは大変好感が持てた.
インドネシアは,パビリオンの外で伝統舞踊のパーフォーマンスがあって,

ポーランド館ではポーランド人の詩人の書いた俳句の日本語と英語の翻訳を書いたカードを一枚選んでとって, もらってよい,というのがあって,僕がとったのは, イェジー・ヤルニェーヴィチというネットで検索しても名前の出てこない詩人の
黄ばんだ葉の上命の線が走る ----僕は閉じる掌をというものだった $^{[1]}$.原文がないので確定 的なことはわからないが,この黄ばんだ葉は Ahorn の葉のことではないか? 命の線とは手相の 命線のことではないか? 「黄ばんだ」は,Złota Polska Jesień (黄金のポーランドの秋) というときの黄色のことなのではないか? もしこれが正しい推測なら, 原文を知らなく ても,僕なら,これは
黄金の葉の上を生命線が走る ----僕は思わず掌を閉じるとでも訳したと思う.
しかし,これに限らず,どの国の展示も壁に書いてあるメッセージの日本語や英語が無神経すぎる. 言語 (ことば) をなめているのではないか. 聞こえてくる音楽も,インドネシア館でのものはぎりぎりだったとしても (ガムランはいいにしても, そのつなぎでインデイアナジョーンズのハリウッド音楽みたいな下品な, と言ったら言いすぎだとしたら totally uninspiring な,ものが使われていた) 全体としては最悪としか言いようがなかった.
$[1]$ こう書いたら,後で, 友人の一人から,これは Jerzy Jarniewicz のことではないか,という指摘をうけた.
どの国でも,傍観していると某国のように石器時代人の統治する国になってしまうかもしれない, という可能性が見えてきた今日では, 「石器時代人の言っていることは軽く流す」は,その方が得である, という理由でとるべき態度ではないような気がしきりにしているのだが.
僕は数学者という仕事がら, 沢山のユダヤ系の人とも交流があるし,かつての指導教官の中にも, 指導をされたわけではないけれど師と仰いでいる人の中にもユダヤ系の人がいます. 彼等に対する僕の共感は,専門分野を通じてのものだけでなく, 僕のこういった出自とも関係があるのではないかという気がします. ヨーロッパ系のユダヤ系の人達は,単に「人種」的にユダヤ人であるだけ,という人もいますが, 数百年や千年を生き延びたユダヤ文化の伝統が残っている家の出の人たちであることも少なくないので, そのことの僕の背景文化との類似性 (といってもユダヤ人の人たちの背景文化の時間の重さとくらべたら,僕のそれは無に等しいわけですが... ) に親近感を感じる, ということがあるのかもしれません.
このニュースをドイツのテレビの web 版で見ていたら „Warum ist d-moll so traurig: a f d“ (a f d はニ短調の主和音の構成音の音名) というプラカートを掲げている人がいて,笑ってしまいました.
ドイツでの状況は,もアメリカと同じように,対立は教養人対石器人という図式で起こっていて, ドイツでは,その間の力関係がアメリカと若干異なる, というように理解できるかもしれません.AfD だってアメリカの某政党よりちょっとは知的に思えます. といっても,ちょっと知的に見えるのは党首のおばさんがそう見えることもある,ということにすぎないのかもしれませんが.
ちなみに,ニ短調は悲しかったり残念だったりもしますが, 夜の女王のアリアのように危険に攻撃的になることもあります.
(https://qr.ae/pYW4Uh へのコメントから)
この二つは全く違います.多項式は,その式を表わす記号からなる記号列です. これに対して,ある多項式に対応する多項式関数は,例えば実数の範囲で考えているのなら, それぞれの実数に対して,この多項式の変数に,その実数を代入した (計算) 結果を, 返してくれるような関数,のことです.
これが書かれていたのは僕がヨーロッパに住んでいた時期だったので, リアルタイムには読んでいなくて,短期帰国したときに断片的に目にしていただけだったのです.
読んでみて思ったことの一つは, さそうあきらの『さよなら群青』が『わたしは真悟』を下敷きにして書かれているのではないか, ということでした.下敷きと言っても類似性は部分的に contravariant な歪んだものになっている,というべきかもしれませんが.『さよなら群青』は『ダフネスとクロエ』や 『潮騒』とのもっとストレートな関係$^{[1]}$ も指摘できるのですが, 『わたしは真悟』も含めて,これらの作品について,もう一度考えて直してみてもいいように思えます.
『わたしは慎吾』品の第I巻は,2018年にフランスの Festival de bande-dessinée d’Angoulême で Prix du patrimoine (heritage prize (?)) を受賞しているということですが, 第I巻だけが,というのは,なかなか微妙です. この微妙さは,この漫画の第2部で,当時1980年代のアメリカでの Japan bashing を反映している, と思われる, イギリスでのエピソード (日本人たちがロンドンで身の危険を伴なうような過激なバッシングにあう) が描かれていることを知っていると, その意味が分かると思うのですが,英語の Wikipedia にも, ドイツ語の Wikipedia にも,このエピソードに関する記述が全くない,という不思議な現象も起っています.
英語ではしょうがないにしても,ドイツの Wikipedia で,このことを客観的分析的に記述することのできる筆者がいないことは, 私にはとても不満に思えます.
[1] 伯母野山日記 2012 -- 2016, さよなら群青
人類が滅亡するにちがいないことの大きな理由は, ホモサピエンスが全体として, 新石器時代くらいからそれほど変ることができないでいることだろう.もちろん,その理由は, 人類の文明や技術が,その頃から人類の進化を待たずにに現在までに急速に進歩してしまったからなのだが, その結果, 多数決をしてしまうと,石器時代の価値観や, それよりの時代から継承している本能という,時代錯誤で物事が決まってしまう.事実の例証と言ったのは, このことの例証という意味である.
もちろん,昨今の滅亡は免れないとは思うが, それだけでなく,人類の知性の尊厳を保って滅亡する, などという理想も到底達成できないものになってしまっているのではないのではないか,と思えてくる.
久しぶりに目を通してみたらいくつか書きそこない等 (手書きなので typos ではない) が見付かったのでが見つかったので,少し補筆訂正してある.
同じようなことは,ChatGPT についても言えるように思える.ChatGPT で面白いのは, それ自身もそうだが,それにも増して, ホモサピエンスの (集団として,あるいは各個体の) ChatGPT への対処の仕方の方であるように思える.
先のパンデミックでは,タイムスパンが政治家の任期の長さと compatible だったので,政治家が状況を本当には理解していなくても, 比較的容易に科学者の助言を聞くことのできる流れができていたのですが, 地球の気候変動では,変化はおそろしく速いといっても, 政治家の任期の長さははるかに越えているので,政治家が自分の政治生命の存続のために, 科学者の助言を聞くことがプラスになる,と判断しにくく,このこともあって, 事態はかなり深刻に思えます.
これは,20世紀の後半に,科学者たちによる,かなり的確な (なぜそう結論しているのか, ということについての理解のできるはずの明確な説明つきの) 指摘があったにもかかわらず, アメリカの政治家の過半数が, 気候変動の事実ないし (その時点で認識できたはずの) 可能性を無視し続けた (そして他の国の政治家の大多数もこれに倣って似たり寄ったりの行動に出ていた) ことを思い出すと理解できると思います.
民主主義は,dictatorship に比べれば格段良いシステムだとは思いますし,現在の dictatorships の下での気候変動対策は無きがごとしですが,気候変動などの科学的な事象に対して, 民主主義のシステムで人類が正しい決断をするためには, 人類の過半数が,例えばネイピア数などの基本概念を正しく理解している必要があります. このことの実現は,現状を見ると,絶望的に難しい,というかほとんど不可能なことのように思えます.
Greta Thunberg の言った言葉に,Politicians should listen to what the scientists are saying about how to address the crisis というのがありますが, これは,理解できなくても彼等の言う結論を受け入れろ,ということでしょう. Scientists たちは,真理の追究ということに関しては信用ができること多いかもしれないけれど, 彼等の言う結論を理解できずに受け入れるというのは,受け入れる側のアクションとしては, 巫女の告げる神託を受け入れる, というのと何等変らないものになってしまい,人類の理性の尊厳を踏みにじる行為という意味では, 気候変動で何が起っているか全く分らずに,何もしなかったり,状況の悪化に手を貸してしまうのと, 似たりよったりであるような気もします.
それは別としても,scientists の言う提案は,必ずしも愚民にも実行可能な形のものではないので, 政治が scientists の言うことをよく理解した上で,これを実行可能だが (昨今, 各国の政府や国際協定などの打ち出しているような) 腑抜けな内容になってはいないものに翻案した上で施行するのでなければ, 意味を持ちえないようにも思えます.
そういうわけで,私は,人類の未来に対して,明かるい展望は殆ど持てないでいるのですが, 最近,一つの希望が見え初めているように思えます.それは,近未来の AI が, 近未来の人類を,飼育育成することで,危機を回避してくれる,ということの可能性です. 人類が,滅亡に突き進んでいて,この軌道修正ができないでいるのは,一つには, 上で言ったように, 人類が,過半数原理をクリアするだけの知性の平均値を達成できないでいるからなのでしょうが, 実は,その主要な原因は, 人類が人類になる前の時代から持ち越している本能や戦争などの滑稽な集団的な行動様式が邪魔をしている, ということがあるのだろうと思います. 未来の AI が知らない間に人類を品種改良を施してそのような障害を取り除いて, 同時に気候変動をはじめとする問題の対策を人類と共存する形で遂行してくれる, というのは可能な未来世界の一つであるように思えます.
でもこれでは,共存と言っても,究極の dictatorship ではないか,と言う人もあるかもしれません. そうだとしても,未来の AI は,現在の擬似 AI からの bootstrapping という側面も持つかもしれないとしても,人類の知性の作り上げたものである, とは言うことができるはずなので,その意味では,人類の知性の尊厳は保たれることになる, と考えてもよいのではないでしょうか.
数日前 (これを書いているのは 2024年の5月末です) に, ヨーロッパから訪ねてきた友人と彼の家族と一緒に奈良観光をしてきたのですが, 奈良の鹿たちの人間との共存は,未来の AI と共存している未来の人類を暗示しているかもしない, と思ったのでした.
ところで,私がここで何度か使った, 「人類の知性の尊厳」という表現は,19世紀のドイツの数学者ヤコビ (C.Gustav Jacobi) の言った言葉です. 彼の,1830年のフランスの数学者ルジャンドルにあてた,フランス語で書かれた手紙で, 「フーリエ氏が、数学の主要目的は、一般の用に供することと、 自然現象の解明にあると言つたといふのが本当だとしても、 彼ほどの哲学者が、科学の唯一の目的が人類の知性の尊厳にあることを知らぬはずはないし、 だから、その意味で数に関する問題が多体系の問題と同じくらい重要なことも知らぬはずはないであらう。 」と言っています.
実は,私は Quora などで書いた,主に数学に関する文章書き直したものを集めた 『数学の質問に答えてみる』という題の本の上梓を予定しています.最も, Quora での文章については,質問文には,私の copyright はないので,もとの質問ではなく, 私の答えから reverse engineer した質問文になっているのですが.もう本文自体は完成していて, 更なる推敲をすればよいところまで来ているのですが, 今あなたの読んでいるこのいささか重いものになってしまった答えを, この本の質問と答えのセクションの最後に加えようかと思っています.
Quora にはちょっと時間をとりすぎてしまったところもあります. 未発表の論文も沢山溜まってしまっているので, この答えと, もう一つの, 数学的に少し重い答 (これはここではなく数学の一般向けの雑誌に載せてもらうことになるかもしれません) を最後として, 少しお休みをしたいと思っています. しばらくしてまだ人類が滅んでいなようだったらまた再開することもあるかもしれません.
私の理解では,数学は, 本質を理解するための (究極の) 方法 (と,そのような方法の考察としての方法論 (methodology)) である.しかし, この種のタイトルの本を書く人の多くにとって,数学は, (精密な) 計算の道具にすぎないのではないだろうか. そして,まさに,このことが,私を落胆させる本の内容の背景となっているのではないか, という気がする.
AquaSKK はまあ問題なく使えているし,emacs での user 辞書を参照させることもできているのだが, emacs lisp のコードを辞書に書くことはできないので,これが僕にとってはネックとなってはいる. たとえば,僕の SKK の辞書には,▽しょうわ3ねん[return] で
(concat(int-to-string(+(string-to-number (car skk-num-list)) 1925)) "年")が呼びだされるようになっていて,“1928年” という変換がされることになるのだが, これは AquaSKK では使えない. もちろん似たことができるようになっていることは, 一般ユーザーにとっては大きなセキュリティーホールになってしまうわけなので, この点を改良してもらえるチャンスはほとんどないだろう.
実用上では,AquaSKK での変換で対応できなくなったところで,emacs の走っている terminal に行って, ここでの SKK で変換したものをコピーして(emacs の kill 関連のコマンドは MacOS の cut buffer に文字列を置くように書き換えてある) MacOS 上のAquaSKK を使っている app で paste すればいいので,それほど手間にはならないのだが.
Jim Jarmusch の Dead Man の始まりのシーンのようだ.
駅で待合せて,昼食に向かった.このまえ Catalina たちと行ったレストランにしようと思っていたのだが,残念ながら 定休日だったので,漬物とごはんの「バイキング」のレストランに入った. 食事のときに話していたら,Vittoria に僕の言ったことが David の言うことと全く同じだ,と言われた. どこかで同じことを言われたことがあると思って記憶をたどってみたら,これはずいぶん昔に Joan の奥さんに言われたのだった.David も Joan も数学者でカタルニア人なのだが,これは, 数学者は発想が似ているので,同じようなことを言ってしまうということなのか, それとも,僕がカタルニア人的発想をする,ということなのか.
これは「ドキュメンタリ」ではなく「小説な」のだが, リサーチは綿密にしてあって, 史実とは違っても,記録に残っている何かに対応していることしか書かれていないようには思える. しかし,逆に,史実どうり,ということではまったくない.
Göldel が Kafka を好んでいたというのが出てくるが,これは本当にそうだったのだろうか. Goldstein がそう書いているみたいだが,彼女の書くことはあまり信用できないような 気がする.と思って調べてみたら,Princeton, 4./VII. 1962 の日付のある彼の母親にあてた手紙で Gödel は Kafka を最近発見した,と書いている.でも “Planck oder ...” のエピソードで Gödel がこれを 言うのは,1945年のある日だし,Gödel が有名な “The more I think about language, the more it amazes me that people ever understand each other at all.” をドイツ語で言うシーンも同じエピソードで出てくるが, これも,この表明の出典は多分 Hao Wang の “Reflection ...” で,これが書かれたのは 1980年代である.
... まったくもって不愉快だ!!!
この国には職人はいても芸術家はいない!
道具はあっても美術品はない!
すべてが遊びにとどまり高尚なものの存在に気付こうとさえしないのだッ!!!
--- 杉浦日向子,『東のエデン』,(1986)

--- Donald Richie, The Inland Sea (1971)
群とは, 群の公理を満たす構造だが, この公理は,述語論理の有限個の論理式の集まりとして書けるものである. たとえば,群の演算を記号 $\circ$ で表わしているとして,単位元の存在公理は,$\exists x\forall y\, (x\circ y=y\land y\circ x= y)$ という論理式で書ける.無限群 (群の underlyning set が無限であるような群) は存在する. 例えば,$\langle{\mathbb{R}, +}\rangle\$ はそのようなものである.ここで Upward Löwenheim-Skolem Theorem と呼ばれる定理を応用する.
定理 (Upward Löwenheim-Skolem Theorem). 述語論理の (有限個または可算無限個の公理からなる) 理論 $T$ が無限構造をモデルとして持てば, 任意の無限濃度をサイズとして持つ $T$ のモデルが存在する.
この定理により, 任意の無限濃度の群が存在することが帰結できる.特に異る濃度の群は同型でないから, 互いに同型でない群がクラス個存在することが ... 分かりそうなのだが,しかし, ここで,群の同型タイプ (isomorphism types) の全体という対象をどう捉えたらいいのか, そもそも,これを捉えることができるのか, という問題が出てきてしまう.
群 $G$ を一つとったときに,$G$ (の underlying set) と等濃度の集合はクラス個あるので, それらに $G$ の構造をコピーしたものを考えると, ある群と同型な群の全体は真のクラスになることがわかるので, 群の同型タイプの全体を考えようとすると, クラスのクラスを考えなくてはいけなくなってしまうが,クラスのクラスは (Zermelo-Fraenkel 集合論の枠組では,そのままでは) 扱かうことのできない対象である.
北米で Scott's trick と呼ばれることもあるテクニックを使うことで, この問題を回避することができる. この Scott は, コンピュータサイエンスの人は名前を知っているはずの Dana Scott である.
正則性の公理から,集合論の universe $\mathbf{V}$ (全ての集合からなるクラス) は, 現代の集合論の記法では,$V_\alpha$, $\alpha\in\mathsf{On}$ と表わされる集合の上昇列 (von Neumann hierarchy) の和として表わせる. $\mathbf{V}=\bigcup_{\alpha\in\mathsf{On}}V_\alpha$ である.ただし, $\mathsf{On}$ で順序数の全体からなるクラスを表わしている. 群 $G$ に対し,$\alpha_G$ を, $V_\alpha$ が $G$ と同型な群を含むような $\alpha$ のうち最小のもの,として, $I_G=\{{H}\,:\,{H\in V_{\alpha_G}, G\cong H}\}$ として,$\mathcal{G}=\{{I_G}\,:\,{G\mbox{ は群}}\}$ とする. この $\mathcal{G}$ を群の isomorphism types 全体のクラスの代用品にする, というのがそのアイデアである.
各集合 $I_G$ から,要素を一つ選択してそれらを集めたクラスを考えればいいではないか, と思うかもしれないが,それをしようとすると,クラス個の選択をしなくてはならなくなり, これは,選択公理を仮定しているとしても,選択公理の適用範囲外だし,そもそも Zermelo-Fraenkel 集合論の枠組では,そのような選択を許す選択公理の拡張版の一般形を記述することすらできない. そのようなわけで,集合 $I_G$ を $G$ の ispmorphism type の代表元の代用品として扱かう, というトリックが,ぎりぎりのところで, この isomorphism types の全体のクラスを扱うことができる, ということの保証となっているわけなのである.
$\mathcal{G}$ が集合でないことは, 次のようにして分かる.順序数の全体 $\mathbf{On}$ は真のクラスになることは既知とする. 基数の全体 $\mathbf{Cn}$ も真のクラスである: $\mathbf{Cn}$ の要素は, 順序数で昇順に添字つけできるのでもし $\mathbf{Cn}$ が集合だとすると, $\mathbf{On}$ も集合になってしまい矛盾である. ここで,$\mathcal{G}$ から $\mathbf{Cn}$ への写像を, $I_G$ に対し,$I_G$ の要素の濃度 (つまり $G$ の濃度) を対応させる関数とすると, 上の Upward Löwenheim-Skolem Theorem から, この関数は上射になるから, もし $\mathcal{G}$ が集合だとすると,$\mathbf{Cn}$ も集合になってしまい,矛盾である.
* * *
上の議論が, 一般の数学者に難しいかもしれない理由としては, Upward Löwenheim-Skolem Theorem という論理学の定理 (より正確には, 論理学と集合論の間にある定理と言うべきか) が用いられていることもそうですが, 正則性公理という (「基礎の公理」と呼ばれることもある) 普通の数学ではほとんど使われることのない集合論の公理が使われていることと, 置換公理と呼ばれる Zermelo-Fraenkel 集合論を,Zermelo 集合論でないものにしている公理が何度か使われていることもあるでしょう.
ただし,この証明が本質的に Aermelo-Fraenkel 集合論で遂行されているとしても, 「... が集合でない」, という形の主張は,一旦 Zermelo-Fraenkel 集合論でこれが確立した後には, この結論自身は,Zermelo-Fraenkel 集合論でも集合であることが証明できないのだから, その部分体系であるところの Zermalo 集合論は,このことは当然証明できない.という議論で Zermelo 集合論に戻すことができます.
一般に,同値類の集合の各々から,代表元をとり,それを集めたものを使って商構造を作る, という構成法では, 「代表元をとってきて,それを集める」というところで選択公理が必要になってしまうのですが, 選択公理を仮定しない数学では,この「代表元をとってきて」という操作をさぼって, 同値類たちを全部集めたものを商構造の underlying set とする,という $\mathcal{G}$ でも採用された構成法が,至る所で活躍することになります.
なお,上では, 群の全体のクラスだけではなく, 構造の集まりからなるクラスが集合でないこと示すときの汎用性のある議論を選んだため, Upward Löwenheim-Skolem Theorem などという飛び道具を使ってしまっていますが, 群に特化した議論では, 群の全体が,直積に関して閉じていることを知っていれば,ある有限群 $G$ をとってきて, 各々の基数 $\kappa$ に対し, $\kappa$ 個の $G$ のコピーの直積 $G_\kappa$ を (たとえば, 順序数だけを使ってこの構成を遂行することで, 選択公理を用いずに構成の結果が一意に決まるように工夫できるので,そのようなものとして) 作れば, $\{{G_\kappa}\,:\,{\kappa\in\mathsf{Cn}}\}$ は,互いに同型でない群からなるクラスになるので, このことから群の全体が (本質的に) クラスであることの証明ができます.
My future arXiv posts will be also provided with (correctly spelled) my name and and abstract in Japanese.
The following is the first test of such a type-setting (of an extended version of a paper which at the moment I am not going to post at arXiv):

At first this spiral form of representation did not appeal to me at all. But then I realized that it can be conceived as spiral staircase looked up from the ground floor. $\omega^\omega$ is then the ceiling of the top floor of this building much lower than the skyscrapers called large cardinals. Of course, large cardinals are too high, and spiral staircases are simply useless in them.
This idea brought me back to a memory of my childhood when my mother once brought me to the office of the company where my father worked. The office was in a building which had (for the 4 years old child) huge spiral staircase and the child was perplexed since he thought he was just walking round but he was apparently climbing up.
If my memory is correct, the building was in Ôtsuka, and according to another Wikipedia article, Ôtsuka was a district of Tokyo heavily destroyed by American aerial bombardment. The building must have been one of the few in the area which survived the second world war.
Perhaps this Milner-Rado Paradox type shock was one of the formative experiences which brought me to set theory.
冗談でそう言ってはみたが, 実際には,気候変動の解決を個人のモラルで解決すべき問題として捉えようとする, というのは,そもそも完全に間違っているだろう. もし,気候変動による人類の滅亡を本当に阻止したいのなら, やらなくてはいけないことは,まず第一には,戦争のような, 無駄に厖大な二酸化炭素輩出やリソースの消耗をするアクションを起こそうとするような, 旧石器時代タイプのリーダーや独裁者を消滅させることだろう.しかし, そのような対策を人類がとれるとはとても思えないし, 仮にそのような対策がとれたとしたら. それは,それ自体 (旧石器時代由来の) モラルの壊滅でもあるだろう.
今 AI (と現在言われているものの延長線上にある何か) が人類を飼育管理するようになる, という未来の可能性の一つが見えてきているように思えるが,この未来の AI が上で言ったような, 対策を行なってくれる,という可能性はあるようには思える. 人類だって,ちょっと時間をかけてはいるが,一部の家畜の性格を 「獰猛」なものから「温和」なものに変えてゆくことができているのだから,未来の AI が,ホモサピエンスの習性に修正を加える,ということは,もっと短期間にも可能かもしれない.
独裁国家の国民を見ていると,人間は,少なくともその過半数は, 案外飼育管理されるのが好きな動物かもしれないので, 飼育するのが,AI という神なら,人類は結構納得して飼育管理されるのではないだろうか.
しかし,そもそも,そのような未来の展開が可能になるだけの時間はホモサピエンスに残っているのか, という疑問も残る.でも,それなら,ホモサピエンスが滅んで,この未来の AI が 「人間のない神」として残る,という筋書はどうだろうか?
現在では,emacs は国際化していて,特別な version を install しなくても, 日本語だけでなく,ほとんどどの言語でも処理できるようになっている.
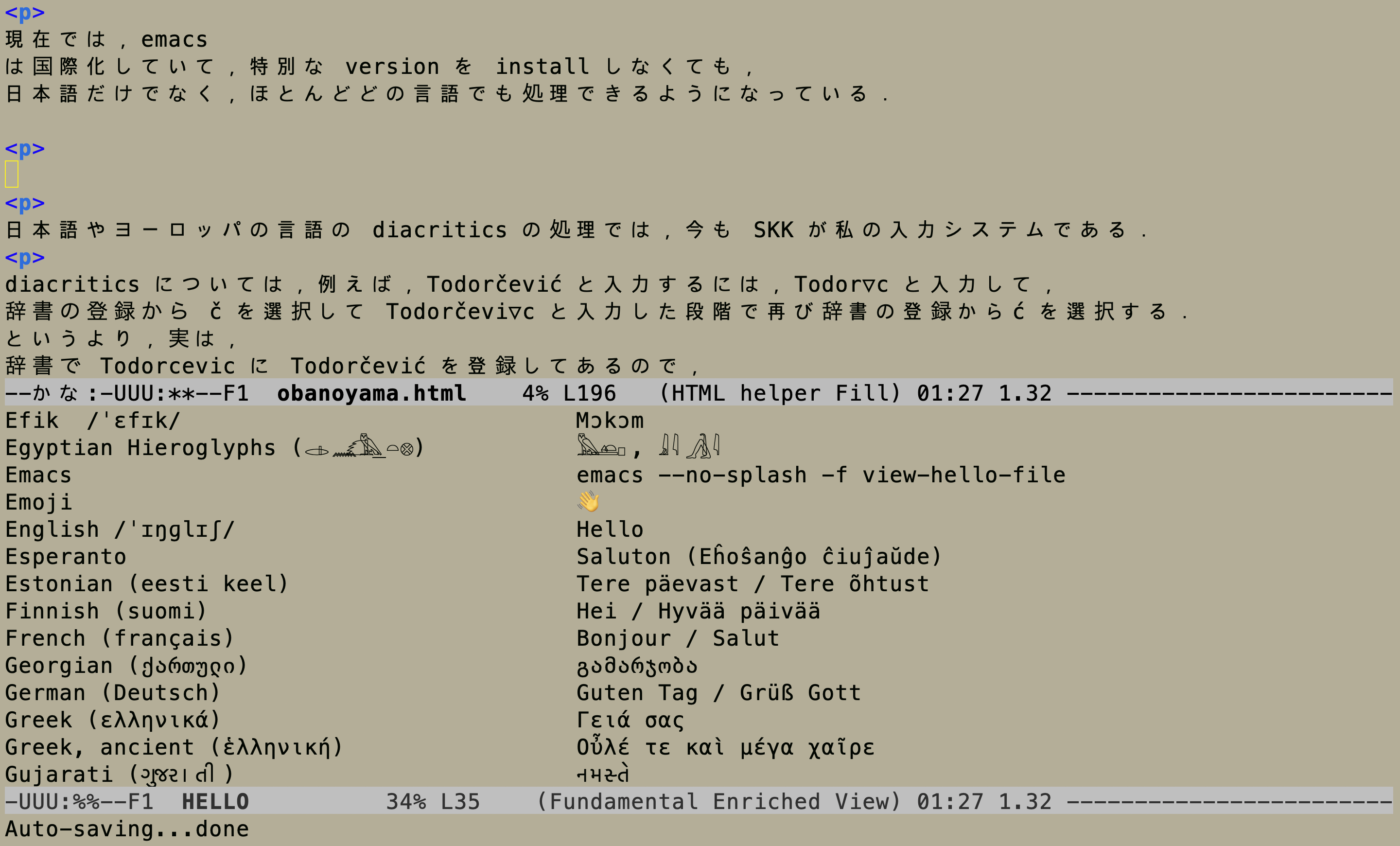
diacritics については,例えば,Todorčević と入力するには,Todor▽c と入力して, 辞書の登録から č を選択して Todorčevi▽c と入力した段階で再び辞書の登録からć を選択する. というより,実は, 辞書で Todorcevic に Todorčević を登録してあるので, ▽Todor[tab][space][return] で入力が完了する.
“𝑎 ∈ 𝓕 ” の入力は,▽matha[space]▽in[space]▽calF[space] で実現できる.
アメリカに住んでいる人と天気の話をすることが多いので, ▽せっし12[space] で 「華氏53.6度」 「53.6°F」「12°C」「摂氏12度」などが出力できるようにしてある (これは一行の Emacs Lisp code を SKK の辞書に埋め込むことで実現できる)
今のところ韓国語の入力は,MacOS のinput method とvirtual keyboard を使ってやっているが,これも,上のような方法を使って,例えば skk で,▽Krpan で 방 が出力できる,というような設定ができればと思っている.
日本語では, あまりうまくゆかないのですが,ヨーロッパの言葉や英語では, 数学に出てくる対象を主語にして,この対象の視点から話す,という表現の仕方が可能です.と書いたところ,
数学でも 「実数の気持ちになって考えろ」というのがあるんですね。 そういえば化学に「電子の気持ちになってry」という決めゼリフがあることは Quora でも時々出ますね。 他にもあるのかな?というコメントをいただいたのだが, どうも「実数の気持ちになって考えろ」は違うような気がしたので, 解答を補筆してみたのだが, どうも質問をした方は,これを,「実数が自分で考える」と考えることと, 「実数の立場になって」(人間が) 考える,という違いの問題,と解釈されたようだ. そこで,以下は,その解釈に対する解答:
自分が実数の立場で考えるのと,実数が自分で考えることの間にはそれほど差がないのではないかと思いますが,私が問題にしたのは,個々の実数が普通の意味での一つの数という対象として数学的思索をめぐらすわけではない,ということです.回答にも書いたように,数学の全知識 (人間が現時点で知っている知識だけでなくもし神がいれば知っているようなすべての知識) を無限小数としてコードするような実数が (数学の意味で) 存在して,更にそのような存在の極北 (の更に彼方) には 0# が存在したりするわけですが,これは, (これも物理的な意味ではなく数学の意味での) 実数直線上の点としての,この実数ではなく,その実数に特定のやり方で構造的にコードされた知識です.普通の数学での,ある実数の実数直線上での意味を考えているのは,この実数自身でなく,むしろ,この実数を含む連続体 (すべての実数の全体に四則演算などの canonical な数学的な operations や relations を付け加えて得られる構造) です.しかし,ここでの問題は,むしろ「日本人の気持になって考えろ」というような, 全体主義的な表現が自然に書けてしまう日本語の問題なのかもしれない.もし 「実数の気持になって考えろ」が, この「日本人の気持になって考えろ」のような意味で formulate されて されているのだとしても,collective としての “reals” はその上の構造なしには, 単なる集合である.やはり,考えるには構造が必要に思えるのだが ... Collective としての “reals” のこととしても,これはやはり「連続体の気持になって考えろ」と表現したい気がする.
* * *
現代の数学を,現代の意味での論理学上で展開する場合の,「背理法」の正しさの説明をしてみようと思います.数学的な「証明」は不可能です:数学の基礎を確立するときには,まず何もないところに論理の体系を設定して,そこで数学の公理系を導入して,その公理系からの,論理の体系での推論によって証明される定理からなる理論体系を構築してゆく,という手順をとらざるを得ないので,この,まだ何もないところに論理の体系を確立するときには,論理の体系を描き表すための記号の扱いに関する基礎事項以外には,証明で使える仮定や手立ては,まだ何もないからです.
さて,この論理の体系 (この体系を 𝓛 と呼ぶことにします.“logic” の頭文字からの記号の選択です) が確立されたとして,数学の公理系 𝑇 を設定して,そこから数学的な命題を証明してゆくことを考えます.そのような文脈で用いられる論理の体系 𝓛 で,ある公理系 𝑆 が矛盾する,とは,𝑆 から,どんな命題も導けてしまうことです.どんな命題も導けることは,大層具合がよいように思えるかもしれませんが,ある命題が φ が 𝑆 から導けたとしても,その否定 ¬ φ もそれから導けてしまうので,φ が正しいのか ¬ φ が正しいのか,という判定には何の役にも立たないものになってしまいます.
この,矛盾する公理系からは何でも導ける,ということは,論理学を勉強していない人は理解できていないことかもしれないので,まず,ここから説明しなくてはいけないかもしれません.論理の体系 𝓛 が確立された,というときには,𝓛 での公理系 𝑇 から,ある命題が証明される,ということが何か,という定義がきちんと与えられた,ということを含んでいます.この 𝓛 での証明の概念の意味で命題 φ が証明された,ということを,𝑇 ⊢ φ または,これが体系 𝓛 でなされていることを強調するために,$T\ \vdash_{\cal L}\,$φ と書くことにします — これは証明論 (Proof Theory) と呼ばれる論理の体系たちを研究する数学の分野で標準的に用いられる記号です.以下では subscript 𝓛 は,$\LaTeX$ で書かなくてはならなくて煩雑になるので,省略することにします.
このような証明の体系の持つべき性質の一つに,演繹定理 (Deduction Theorem) と呼ばれるものがあります.これは,証明可能の概念 $\vdash_{\cal L}$ と, 論理演算子「ならば」 ⭢ の間の整合性を主張するもので,
すべての理論 𝑆 と命題 φ, ψ に対し,𝑆+φ ⊢ ψ と 𝑆 ⊢ (φ ⭢ ψ) は同値である
というものです.ただし,𝑆+φ で公理系 𝑆 に命題 φ を付け加えて得られる公理系を表わしています.
我々の論理の体系 𝓛 も妥当に導入されていて,この演繹定理を満たすもの,
とします.このとき,明らかに矛盾する何らかの命題 (例えば,この論理の体系で考えている理論に 0
という定数記号が入っていて,“(0=0)” が論理公理 (である / から演繹できる) ときの “(0≠0)” ) が 公理系 𝑆 から証明できるとします.つまり 𝑆 ⊢ (0≠0) です.ここで,任意の命題 φ について,((0≠0) ⭢ φ) は恒真な命題になるので (implication で前提が偽の命題は恒真になりますが,そのことはこの論理体系 𝓛 にも反映されている,と仮定しています),𝑆 ⊢ ((0≠0) ⭢ φ) となりますが,演繹定理から,𝑆+(0≠0) ⊢ φ が導けます.ところが,(0≠0) は 𝑆 から証明できるのだったから,証明の前提から外すことができて,𝑆 ⊢ φ が言えることがわかります.φ は任意だったので,矛盾する公理系 𝑆 からは何でも導き出せてしまうことの証明 (説明) が得られたことになります.
論理の体系 𝓛 は,次の性質も満たすことを仮定します.
(*) すべての理論 𝑆 と命題 φ, ψ に対し,𝑆+φ ⊢ ψ と 𝑆+ ¬φ ⊢ ψ が成り立つときには,𝑆 ⊢ ψ が成り立つ
これは,「理論 𝑆 のもとで,φ を仮定したときに ψ が成り立ち,φ の否定を仮定したときにも ψ が成り立つなら,φ の成否にかかわらず,ψ が成り立つ」ということを表現する性質となっていると考えられるので,これが成り立つという仮定も,妥当なものです.
さて,今,任意の公理系 𝑇 から出発して 𝓛 で議論をするとします.ここで,𝑇 に,ある命題 の否定 ¬φ を加えてできる公理系 𝑇 + ¬φ から,矛盾,例えば (0≠0) が証明できた,とします.このときには,上で見たように 𝑇 + ¬φ から何でも証明できるので,特に,𝑇 + ¬φ ⊢ φ が言えます.一方,(φ ⭢ φ) は恒真命題なので (𝓛 が妥当な論理の体系として導入されているなら) 𝑇 ⊢ (φ ⭢ φ) が言えます.したがって,演繹定理から,𝑇 + φ ⊢ φ が帰結できますから,ここで,(*) を使うと,𝑇 ⊢ φ が言えたことになります.
証明ではなく (妥当性の) 説明だと言いましたが,あえて定理と証明の形に書くとすると,上で議論したことは,以下の定理の証明として,理解することができます.
定理. ある論理の体系 𝓛 で導入された証明の概念が,演繹定理と (*) を満たし,上で出てきた形の命題論理の意味で恒真な命題を導くなら,この論理の体系 𝓛 では背理法の原理が成り立つ.
通常,数学では,「絶対的な真理」を想定した,古典論理と呼ばれる,上の定理でのような性質を持つ論理が用いられるので,背理法は縦横に用いられることになるのですが,「絶対的な真理」の概念を放棄して,しかも数学は放棄しない,という立場も色々とあって,そのような立場に対応する,普通と違う論理や数学も研究されています.
直感論理と呼ばれる論理は,そのような論理体系の代表的なものです.(直感論理の上に構築される直観主義数学というものもありますが,これは,構築の仕方に独特の「くせ」のあるもので,ここでは,それについては議論していません).この直感論理は,ごく大雑把な説明ではありますが,ある命題 φ が正しい,ということを,φ の正しさを確証できる手立てを我々が持っている,ことだと考える,という解釈に対応するような論理的推論を許す証明の体系になっています.そのような論理体系では,命題 φ の否定 ¬φ の解釈は,「φ とならないことの正しさを確証する手立てを我々が持っている」ということになるわけですが,このような解釈で考えると,背理法の原理は一般には成り立たないものになります: もし,¬φ から矛盾が導かれたとすると,の解釈では,それは,「φ とならないことの正しさを確証する手立てを我々が持っていることから矛盾が導かれる」ということですが,このことは必ずしも 「φ の正しさを確証する手立てを我々が持っている」ことを帰結しないからです.これに対して,背理法の特別の場合である,「否定の証明」つまり,「φ だと仮定すると矛盾が生じる,したがって ¬ φ である」というパターンの推論は,直感論理でも許容される推論になります.「 φ として矛盾が導ける」ことの例となっている矛盾の証明が得られたときには,この証明自身が「φ とならないことの正しさの確証」になっているからです.
日本の文化は,
絶対的な真理を司る一つの神を持たない (というより言語に単数と複数の区別すらない) ので,日本人の中には,絶対的な真理を擁護する古典論理に基づく数学に懐疑を抱く人が少なくないようです.しかし,このような背景から,直感論理を採用したいと思っている日本人の人たちの多くは,この,直感論論理でも「否定の証明」は許容される,という事実を,きちんと認識していないことが多いのではないかと思います.
井上尚夫さんの完全な解答 が既にあるので, 以下はどちらかというと蛇足とも言えるものです.井上さんの解答でもそうですが, この一意性証明のキーになる 「二つ数の積 𝑎𝑏 を素数 𝑝 が割り切るとき, 𝑝 は, 𝑎 か 𝑏 の少なくとも片方を割り切る」という Euclid の補題とも呼ばれることのある命題の証明には,Bézout の補題 (の特別の場合: 井上さんの解答で 「定理」と呼ばれている主張) を用いる証明が色々なところに書かれていると思います. これは,エレガントな証明と言えるのですが,この証明は,「Bézout の補題をここで応用する」, というオラクルがなければ,自然に思いつけるものではないので, 素因数分解の証明の再現を初心者が素手で試みるときに挫折してしまう場所になっています. このEuclid の補題の証明を Bézout の補題なしに素手で (ある程度) 簡素に証明できないだろうか, とずっとおもっていたのですが,この質問を見て再度試みてみたところ, 少し長くなるけれど, straightforward な証明が見つかったので,それを以下に書き出しておこうと思います.
以下では,「自然数 𝑛 が, 自然数 𝑚 を割り切る (𝑛 divides 𝑚)」という主張を 𝑛 ∣ 𝑚 という記号で表しています. これは初等数論などで標準的に用いられる記法です. 𝑛 ∣ 𝑚 でない,という主張は,𝑛 ∤ 𝑚 と表わすことにします.
補題 (Euclid's Lemma). 素数 𝑝 と自然数 𝑎, 𝑏 に対し, 𝑝 ∣ 𝑎𝑏 なら,𝑝 ∣ 𝑎 か 𝑝 ∣ 𝑏 の少なくとも片方が成り立つ .
証明. 主張に反例が存在する,として矛盾を示す.素数 𝑝 と,自然数 𝑎, 𝑏 を,𝑝 ∣ 𝑎𝑏 だが, 𝑝 ∤ 𝑎 かつ 𝑝 ∤ 𝑏 となるようなものとする. 特に,素数 𝑝 は,このような自然数 𝑎, 𝑏 の存在するようなもののうち最小のもとし, そのように固定した 𝑝 に対し,𝑎 と 𝑏 は,𝑎𝑏 が最小になるように選ばれているものとする.
Claim. 𝑎 < 𝑝 かつ 𝑏 < 𝑝 である.
⊢ 自然数 α, β, γ, δ を,𝑎 = α𝑝 + β, 𝑏 = γ𝑝 + δ, β, δ< 𝑝 となるようにとる.仮定から, β≠ 0, δ ≠ 0 である.𝑝 ∤ β かつ 𝑝 ∤ δ に注意する.このとき,𝑎𝑏 = αγ𝑝² + (αδ + βγ)𝑝 +βδ だから, 𝑝 ∣ 𝑎𝑏 から,𝑝 ∣ βδ がわかる.したがって,𝑝, β, δ も反例 となっているから,𝑎𝑏 の最小性から, 𝑎𝑏 ≤ βδ となり,このことから,𝑎 = β, 𝑏 = δ である.⊣
仮定から,𝑎𝑏 = 𝑛𝑝 となる自然数 𝑛 がとれる. 上の Claim から, 𝑛 < 𝑝 である.𝑞 を 𝑛 の素因数の一つとして,𝑛 = 𝑞𝑛' とする.𝑎𝑏 = 𝑞𝑛' 𝑝 である. したがって,𝑝 の最小性から,𝑞 ∣ 𝑎 または,𝑞 ∣ 𝑏 が成り立つが,一般性を失うことなく, 𝑞 ∣ 𝑎 とすると, 𝑎 = 𝑞𝑎' として,𝑎'𝑏 = 𝑛'𝑝 だから,𝑝, 𝑎', 𝑏 も反例となるが,𝑎'𝑏 < 𝑎𝑏 だから, これは 𝑎𝑏 の最小性に矛盾である.q.e.d.
Euclid の補題という名前が示唆するように, この補題には, Bézout の補題より古い証明が既に知られているはずなので, 上の証明と似たものが既に存在するはずだとは思いますが, それにもかかわらず,ここでわざわざ証明を書き出してみたことの理由の一つを挙げるとすれば, それは,上の証明で用いられている,二重帰納法に対応する lexicographical order での最小元に関する無限降下法は, きちんとした日本語で記述されていないことが多いということが言えます.上の証明では, このことは分りやすい言葉できちんと記述されていると思います.
It is easy to see that the uniqueness of prime factorization follows form the 補題 above:
Theorem. For any $n\in\mathbb{N}\setminus2$, there are primes $p_0\lt p_1\lt\cdots\lt p_{n-1}$ and positive integers $\ell_0,\cdots,\ell_{n-1}$ such that
(*) $n=(p_0)^{\ell_0}\cdot\ \cdots\ \cdot(p_{n-1})^{\ell_{n-1}}$.
For each $n\in\mathbb{N}\setminus\{{0}\}$, the representation (*) of $n$ is unique.
Proof. We first prove existence of a representation of the number $n$ as in (*)
by induction on $n$. If $n=2$ then $2=2^1$ is
a representation of $n$ as in (*). Suppose that for we have a representation as
in (*) for all $m\lt n$. If there is no $1\lt j\lt n$ with $j|n$ then $n$ is a prime
and hence $n-=n^1$ is a representation of $n$ as in (*). Otherwise let $1\lt j\lt n$ be
such that $j|n$. Let $k:=n/j$. Then $n=j\cdot k$. Since $1\lt j$, $k\lt n$, both of $j$ and $k$ have
representations as in (*). By marging these representations we obtain a
representation of $n$.
To prove the uniqunes of (*), we first extend the 補題 above to
Lemma. For any $k\in\mathbb{N}\setminus 2$, positive integers $a_0,\ldots, a_{k-1}$ and a prime $p$, if $p\ |\ a_0\cdot\ \cdots\ \cdot a_{k-1}$ then there is $\ell\lt k$ such that $p\,|\,a_{\ell-1}$.
The lemma above can be proved by induction on $k$ where 補題 serves as the induction beginning with $k=2$ and it is also used in the induction steps.
Returning to the proof of the uniqueness, assume toward a contradiction that some integer $n\geq 2$ has two distinct representations. By multiplying these representations by factors of the form $p^0$ ($=1$), if necessary, where $p$ is a prime, we may assume that there are pairwise different prime numbers $p_0,\ldots, p_{k_1}$ and non negative integers $\ell_0,\ldots,\ell_{k-1}$, $m_0,\ldots,m_{k-1}$ such that $n=(p_0)^{\ell_0}\cdot\ \cdots\ \cdot(p_{k-1})^{\ell_{k-1}} =(p_0)^{m_0}\cdot\ \cdots\ \cdot(p_{k-1})^{m_{k-1}}$ but $\langle{\ell_0,\ldots,\ell_{k-1}}\rangle\not=\langle{m_0,\ldots,m_{k-1}}\rangle$. Without loss of generality, we may assume that $\ell_0\lt m_0$. Then we have $(p_1)^{\ell_1}\cdot\ \cdots\ \cdot(p_{k-1})^{\ell_{k-1}} =n\,/\,(p_0)^{\ell_0}=(p_0)^{m_0-\ell_0}\cdot(p_1)^{m_1}\cdot\ \cdots\ \cdot(p_{k-1})^{m_{k-1}}$. Clearly $p_0\ |\ (p_0)^{m_0-\ell_0}\cdot(p_1)^{m_1}\cdot\ \cdots\ \cdot(p_{k-1})^{m_{k-1}}$. But $p_0 \not|\ (p_1)^{\ell_1}\cdot\ \cdots\ \cdot(p_{k-1})^{\ell_{k-1}}$ by the Lemma above. This is a contradiction. q.e.d.
(この Quora の space では post した text の編集を認めないようなので,post の most recent version は,以下のもの,とすることにする.)
人間が脳を使わなくなっていくことの理由になりえるものは,
ChatGPTをはじめとする“AIサービス” 以外にも色々あるでしょう.
逆に,「ChatGPTをはじめとするAIサービス」は,考えるときの道具の一つとしても使えるので,
そのように活用する人も出てきているでしょう.
そう考えると,「ChatGPTをはじめとするAIサービス」が促進することになるのは,
むしろ,
自分の脳を使って考える人間と全く何も考えない/考えられない人間との間の二極化,
なのではないでしょうか.
現在でも既に,
この二極化がきわめて顕著なものになっていて,
この二種類のホモサピエンスの間のテンションが色々なところで問題を起こしていることを考えると,
これは,かなり深刻な問題である,
と言えると思います.
... もっとも,
全く何も考えない/考えられないホモサピエンスというのは (ホモサピエンスという単語が
「知識の人」という意味なので,「知識」という概念を正しく捉えたときには) 形容矛盾になってしまうかもしれませんが ...
where
(0) ZFC,
(1) ZFC + ∃m (m ⊧ ⌜⌜ZFC⌝⌝),
(2) ZFC + ∃m (m ⊧ ⌜⌜ZFC⌝⌝ ∧ m is an ω-model),
(3) ZFC + ∃m (m ⊧ ⌜⌜ZFC⌝⌝ ∧ m is a transitive ∈ -model),
(α) ZFC + ∃α ∈ On ($V_α$ ⊧ ⌜⌜ZFC⌝⌝),
(κ) ZFC + ∃κ (κ is an inaccessible cardinal).
All the implications are strict. More precisely, for ξ < η ≤ κ, we have:
(*) If (ξ) is consistent, then (ξ) $\not\vdash$ the formula of (η) added to ZFC.
https://fuchino.ddo.jp/notes/woodin-incompl-e.pdf
Note that (1) is equiconsistent with ZFC + ¬ 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜ZFC⌝⌝). (1) is equivalent to ZFC + 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜ZFC⌝⌝).
連続体仮説のように,というのは数学の体系からの独立性が証明された,という意味でしょうか?
「証明が多くの数学者に支持された」というのは,
いずれにしても,あまり意味を持たないことだと思います.証明は正しいか間違っているかのいずれかです.
ある問題 — 仮に,これを S と呼ぶことします — の証明と称するものが発表されて, その問題 S の独立性の証明と称されたものも発表されているとき,考えられるシナリオは, 次のようなものがあると思います:
(A) 両方とも間違っていない場合.この場合,更に2つの subcases が考えられます:
(Aα) S の証明が,実は,S の独立性の証明より強い数学の体系 (公理系) で証明されている場合. これは,十分にあり得ます. たとえば,通常の数学の体系からは連続体仮説は証明できないし否定も証明できないわけですが, 通常の数学の体系に Martin's Maximum という公理を付け加えた体系では, 連続体仮説の否定が証明できるだけでなく,連続体の濃度が ℵ₂ になることが証明できます.
(Aβ) S の証明も,S の独立性の証明も,同じ数学の体系上でなされているとき. このときには,これらの結果から, そこで使われている数学の体系が矛盾していることが証明できたことになります. ゲーデルの不完全性定理は,そのような状況が起こることを完全には否定できない, ということを帰結するので,そんなことは起こることはまずない,と皆が思っていても, 絶対ないということはありえません.ただ,このような場合, 数学が全部全くだめになる,ということはまずなくて,体系に何らかの修正が必要となる, というのがそのことの結末になるでしょう.実は,それに似た状況が既に実際に起こったことがあります. これについては昔,
[1] 渕野昌間違いと真理: 解析学と集合論の場合,数学セミナー 2018 年 9 月号,36–42.
で話したことがあります.なお,ここにリンクしたのは,数学セミナーの記事の拡張版で, 雑誌に掲載されたものには含まれないコメントや証明も含まれています.
(B) S の独立性証明が間違っている場合.これは全くないとは言い切れませんが, 可能性はきわめて低いと思います.独立性証明の場合,他の数学とは違って, ちゃんと論理学の素養のある数学者が研究しているし,独立性というのは普通にあり得ない状況のため, 「普通の」数学でよりずっと厳密にチェックがされていることが多いからです. 以下の場合は,独立性証明が間違っていない場合のみについて考えています.
(C) S の証明が間違っている場合.この場合も,少なくとも二つの subcases が考えられます.
(Cα) この S の証明が全く意味をなさない場合. この場合は「そうですかピリオド」という感じでしかないでしょう.
(Cβ) この S の証明は間違っているが,何らかの修正が可能な場合.この場合の修正としては, さらに二つくらいのシナリオが考えられます:
(Cβℵ) S の主張を変更して多少弱いものにすると,得られていた証明か,その証明の variation がそのような S の variant の証明になる場合.
(Cβℶ) 数学の体系 (公理系) を強めると (例えば,上での例のように Martin's Maximus の仮定を加えると) そこでは,間違っていた証明が修正できて,S が証明できる場合.
(Cβℵ) と (Cβℶ) は,実は殆ど同じことの言い換えとも言えるのですが,(Cβℵ) と解釈できる場合と, (Cβℶ) と解釈できる場合とでは得られた結果の意味は異なるものになります.
最後のケースがもう一つありました.
(D) S の証明は正しいが,それが,通常の数学の体系とは矛盾する別の体系で証明されている場合.
例えば,通常の数学は,選択公理を仮定しますが,選択公理を弱めた Dependent Choice
(DC) という公理を仮定して (この公理があれば,
20世紀の前半くらいまでの古典的な数学の殆どがカバーできます) これに,Axiom
of Determinacy (AD) を加えた体系を考えることがあります.この数学の体系では,
古典的な数学は,通常学校で習う数学と同じように展開できますが,
例えば,指数関数には,次のような,選択公理を仮定したときには成り立たない特徴づけが存在します.
定理.(DC+AD) 任意の関数 𝑓 : ℝ → ℝ⁺ に対し,(1) 𝑓 (1) = 𝑒 ; (2) すべての 𝑥, 𝑦 ∈ ℝ に対し, 𝑓 (𝑥+𝑦) = 𝑓 (𝑥)⋅ 𝑓 (𝑦) が成り立つなら,𝑓 (𝑥)=𝑒ˣ が成り立つ.□
上の定理での,通常の選択公理を仮定する数学でとの違いは,𝑓 の連続性が仮定されていないことです.
選択公理の下では,上の定理の主張は,𝑓 の連続性を仮定しないと間違いです.
これは,DC+AD 「すべての関数が連続である」ことを証明する,
ということではありません (通常の論理と異なる論理の下では
「すべての実数関数が連続である」ということ,あるいは少なくとも連続でないことの証明ができない,
という場合があるみたいですが,ここでは,論理は通常のものです). 上の定理の証明で使われているのは,
DC+AD があると,すべての実数関数は可測になり,ベールの性質も持つ,
ということが帰結できる,という事実です.
[1] Kurt Gödel, What is Cantor's Continuum Problem? (1947/1964), in: S. Feferman et al. ed., Gödel: Collected Works, Vol II. (1995).
で論じています.より現代的な議論は
によくまとめられています.この意味での連続体仮説の解決はまだ最終結果が出ているとはいえないのですが,少なくとも,集合論の公理系を自然に拡張したときには,連続体の濃度は ℵ₁ になるか (つまり連続体仮説が成り立つか), ℵ₂ になるか,あるいは非常に大きなものになるかのどれかである,ということができるという議論が可能なことがわかっています.
[3] Sakaé Fuchino, and André Ottenbreit Maschio Rodrigues, Reflection principles, generic large cardinals, and the Continuum Problem, the Proceedings of the Symposium on Advances in Mathematical Logic 2018, (2022), 1--26.
は,強い (連続体濃度以下,あるいは未満への) 数学的反映原理が成立することを仮定したときに,この,連続体の濃度は ℵ₁ になるか (つまり連続体仮説が成り立つか), ℵ₂ になるか,あるいは非常に大きなものになるかのどれかである,という主張が成り立つ,ということについて議論しています.
なお,ゲーデルがなくなる直前に研究していた $2^{\aleph_0}=\aleph_2$ については,現代では,この等式が,Proper Forcing Axiom とよばれる,(上で言ったような意味で正しいことの議論のできる) 公理からも導かれることが知られています — ゲーデル自身の考えた公理は,Proper Forcing Axiom やそれの variations とは異るものでした.ゲーデルの考えた公理 (の候補たち) についての現代の視点からの研究は,
[5] Jörg Brendle, Paul Larson, and Stevo Todorčević, Rectangular axioms, perfect set properties and decomposition, Bulletin (Académie serbe des sciences et des arts. Classe des sciences mathématiques et naturelles. Sciences mathématiques) of Serbian Academy of Sciences and Arts, No.33 (2008), 91--130.
を参照してください.
上で,Proper Forcing Axiom が正しいことの議論のできる公理だと書きましたが,これについては,[2] や,そこでも引用されている
[5] Sakaé Fuchino, On potential embedding and versions of Martin's axiom, Notre Dame Journal of Logic, Vol.33, No.4, (1992), 481--492.
を参照してください.
連続体問題については,日本でジョークになっていない形で伝えられて,それにもかかわらず,あたかもジョークになっているように扱われている,という,ちょっと痛いジョークがあります.
A: 可算濃度を a として,連続体濃度を c とするとき,この間にある濃度は何か?
B: b に決まっているじゃん.
というものなのですが,これでは,何で,可算濃度を a にして連続濃度を c にしたのか分からなくて全くジョークになっていません.実は,このジョークでの a と c は, (20世紀の前半以前には集合論の研究の中心地だった) ドイツのものだと思われます.ドイツ語で可算性を指す Abzählbarkeit という単語と,連続体 Continuum (これは現代のドイツ語では Kontinuum と綴られますが,例えば Cantor は Continuum と綴っています) という単語の頭文字に由来しています.
上のジョーク (になっていないジョーク) の続きみたいですが,a と b は,現代では (多くの場合 fraktur の字体で 𝔞, 𝔟 として) それぞれ almost disjoint number, bounding number と呼ばれる,連続体の特性数となっているような基数を表わす記号として用いられています.たとえば,上で名前の出た Proper Forcing Axiom の下では,$2^{\aleph_0}=\mathfrak{a}=\mathfrak{b}=\aleph_2$ が成り立ちます.ちなみに,記号 c は,現代でも連続体の濃度 $2^{\aleph_0}$ を表わすのに使われています.この記号を使うと,上の等式は,$\mathfrak{a}=\mathfrak{b}=\mathfrak{c}=\aleph_2$ となります.
この 𝔞, 𝔟 に関して,通常の集合論の公理系で証明できるのは, ℵ₀ < 𝔟 ≤ 𝔞 ≤ 𝔠 だけで,例えば,𝔟 < 𝔞 も,通常の集合論の公理系と抵触しないことが知られています.現代の集合論での連続体問題は,連続体仮説が成り立つかどうか,ということにとどまらず,ここで (定義には踏み込まずに) 述べた 𝔞, 𝔟 を含めた,他の特性数の値などのファクターも含めた,連続体 (ℝ や,それと密接に関連する ${}^\omega\omega$ や ${}^\omega2$ などの類似の構造体) の集合論的性質に関する,もっと複合的で包括的な問題と理解すべきものになっています.
Proposition 1. For 𝑛 ∈ ℕ ,If $\sqrt{n}$ ∉ ℕ, then $\sqrt{n}$ ∉ ℚ.
Proof. **Proof.** Suppose that $\sqrt{n}$ ∉ ℕ but $\sqrt{n}$ ∈ ℚ. Note that then $\sqrt{n}$ > 1. Let 𝑘 ∈ ℕ be such that
(0) 0 < 𝑘 < $\sqrt{n}$ < 𝑘+1
and let
(1) ℓ := 𝑚𝑖𝑛 { 𝑚 ∈ ℕ : 0 < 𝑚, 𝑚 $\sqrt{n}$ ∈ ℕ }.
Then
(2) 0 < ℓ ($\sqrt{n}$ - 𝑘) < ℓ
by (0).
(3) ℓ ($\sqrt{n}$ - 𝑘) = ℓ$\sqrt{n}$ - ℓ𝑘 ∈ ℤ
by (1), and hence ℓ ($\sqrt{n}$ - 𝑘) ∈ ℕ ∖{0} by (the left inequality of) (2).
This is a contradiction to the minimality of ℓ. □
The proposition above is usefull in particular because of the following Corollary:
Corollary 2. For any 𝑛 ∈ ℕ, if there is no 𝑚 ∈ ℕ such that 𝑚² =𝑛, then $\sqrt{n}$ is an irrational number.
By Corollary 2, we see immediately that all of $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$, $\sqrt{6}$, $\sqrt{7}$, etc. are irrational numbers.
(Gödel の,あるいは,ある意味で,これの拡張版となっている Henkin の) 完全性定理は,(一階の論理の証明の体系の意味で) 無矛盾な理論 𝑇 はモデル 𝔄 を持つ.という主張として理解できます.質問での,「完全性定理の対象となる理論はモデルを持ちます」は,このことへの言及と解釈できそうです.モデル理論などで,完全性定理を「普通の数学」として応用する時には,この理解の仕方で十分とも言えるのかもしれませんが,不完全性定理との関連で完全性定理を考えようとするときには,おかしな思い違いに迷い込まないために,もう少し踏み込んだ説明が必要になります:
この「𝑇 はモデル 𝔄 を持つ」ですが,これは表現を変えると,「構造 𝔄 で 𝑇 のモデルになっているようなものが存在する」ということです.しかし,記号の操作だけからなる世界 (超数学 -- meta-mathematics) では,構造 𝔄 の存在に関する議論は行なうことができず,この議論のために,何らかの集合論が背景理論として必要になります.完全性定理を,コンパクト性定理を系として導く定理と考えて,モデル理論での応用を中心に捉えているときには,すべてが通常の集合論の中で展開されている,と考えていれば,このことは問題にならないのですが,この定理を,数学の基礎付けの観点での,一階の述語論理の完全性の保証と考えようとするときには,完全性定理により,それ以上の拡張の必要のないことを保証された述語論理の上に,集合論を構築して,そこで数学を展開する,という流れで数学が構築されることになるので,その集合論で完全性定理が証明されている,というのでは悪循環が起ってしまいます.
この悪循環は完全には回避できないものの,完全性定理を記述したり,証明したりするのに必要な集合論は,通常の集合論の公理系のごく小さな断片からなる弱い体系で十分なことが分っています.たとえば,逆数学 (Reverse Mathematics) とよばれる研究では,非常に弱い二階の算術の基本体系の上で,完全性定理 (の2階算術で可能な定式化の一つ) は,WKL₀ と呼ばれる体系と同値になることが知られています.ただし,WKL₀ での完全性定理は,モデル理論で用いられるような集合論での完全性定理とは同一ではありません.たとえば,非可算な理論に対するモデルの存在 (Henkin の完全性定理) は,ここでは記述すらできない命題になっています.
二階の算術の体系は,通常は二階の論理で定式化されますが,以下の定理2の解説で述べることになるように,これは集合論の命題からなる理論に翻訳できるので,その意味で,弱い集合論と看倣すことができます.
一方,不完全性定理は,(少なくとも Rosser による,その拡張では) 記号の有限列の操作だけからなる世界 (超数学 -- meta-mathematics) での定理です.第二不完全性定理は,𝑇 を具体的に与えられた,十分な数論の展開できる無矛盾な理論とするとき,𝑇 ⊬ 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜𝑇⌝⌝) であることを主張するものです.ここで,𝑇 ⊢ φ (あるいは,𝑇 ⊬ φ) は,(閉)論理式 φ が理論 𝑇 から証明できる (あるいは,できない) ことを表わす記号で,⌜⌜𝑇⌝⌝ は,理論 𝑇, あるいは,理論 𝑇 の生成規則に対応する,理論 𝑇 での対象 (たとえば 𝑇 が数論なら「数」) の名称で,𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜𝑇⌝⌝) は,⌜⌜𝑇⌝⌝ からの矛盾の証明に対応する理論 𝑇 での対象が存在しないことを主張する 𝑇 の言語での閉論理式です.
不完全性定理自身は (第一不完全性定理も含めて) 上で見たように,その主張も,その証明も,その背景理論として,どんな集合論も仮定していないし,モデルについての言及も (主張自身にも,その証明にも) 現れないのですが (上の説明で「理論 𝑇 での対象」という言い方をしましたが,これは,形式的には変数記号として --- ないしは体系に付加された新しい定数記号として --- 表現されているものにすぎません),それでは,不完全性定理は理論のモデルに関する考察とまったく関連を持たないか,というと,そんなこともなくて,以下の3つの例でのような不完全性定理の重要な応用では,この定理は,モデルに関する考察とのからみで用いられています.
なお,以下の証明では,モデルを持つ理論は無矛盾である,という,完全性定理の逆 (健全性定理) も用いられています:
定理 1. 初等数論の命題で,集合論の公理系 ZFC では証明できるが,ペアノの公理系 PA からでは証明できないようなものが存在する.つまり,ZFC は,初等数論の命題に関して,ペアノの公理系 PA より真に強いものになっている.
証明.不完全性定理により,PA ⊬ 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜PA⌝⌝) である.一方,ZFC では,⌜⌜PA⌝⌝ のモデル 〈ℕ,+,・,0,1〉の存在が証明できるので,ZFC ⊢ 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜PA⌝⌝) である.□
上で,完全性定理との関連で,弱い二階の算術の体系 WKL₀ について触れましたが,WKL₀ など, 逆数学で考察される二階の算術の部分体系は,すべて 𝒩 :=〈ℕ ∪ 𝓟 (ℕ), 𝓟 (ℕ), ∈, +,・,0,1〉 をモデルとして持つ一階の論理での理論に翻訳できます.ただし,ここで,𝓟 (ℕ) は 𝒩 の単項関係と考えており,∈ は 𝒩 の二項関係 {〈𝑛,𝑎〉: 𝑛,𝑎 ∈ ℕ ∪ 𝓟 (ℕ), 𝑛 ∈ 𝑎} です.したがって,定理1と全く同じ議論で,次が証明できます.
定理 2. 集合論の公理系 ZFC は,二階の論理で記述できる算術の命題に関して,逆数学で考察される二階の算術のどの部分体系より真に強いものになっている.□
上の定理では, 「二階の論理で記述できる算術の命題」が言及されていますが,古典的な数学のほとんどすべて (たとえば大学の1年で習う微分積分の理論で現れるものすべてを含む) は,二階の論理で記述できる算術の命題として表現することができることに注意しておきます.このことを頭に置くと,上の定理 2は,集合論の公理系は,通常の古典的な数学で表現できる命題に関して,古典的な数学より真に強いものになっていることを主張している,と解釈することもできることがわかります.
次の定理は,巨大基数の理論の入門の講義の最初で必ず言及されるはずのものです:
定理 3. (ZFC が無矛盾だとすると) “強到達不可能基数が存在する” という命題は,ZFC から証明できない.
証明. ZFC ⊢ “強到達不可能基数が存在する” と仮定する.ZFC で議論して,κ を強到達不可能基数とすると V(κ) ⊧ ⌜⌜ZFC⌝⌝ となるので,ZFC ⊢ 𝑐𝑜𝑛𝑠𝑖𝑠(⌜⌜ZFC⌝⌝) が導かれ,不完全性定理から,ZFC は矛盾することが結論されてしまい,定理の仮定に矛盾である.□
戦争行動をする動物としては,蟻などの昆虫も思い浮かぶが, 彼らの戦争をする本能のメカニズムは,これとはちょっと違うのではないだろうか?
この質問の答は全部 utf-8 で書き出したので,別のファイルにはしないで, 以下に添付することにする.今,Axiom of Choice の vaiants の Tychonoff の定理の variants での特徴付けに関する解説論文を書いているところなので,この Quora の解答は,実は,それとも連動している. :
ℝ や ℂ では,可算な稠密部分集合がとれて (例えば,ℝ では ℚ,ℂ では,𝑄:={ 𝑞 + 𝑟𝑖 : 𝑞, 𝑟 ∈ ℚ } など ),この稠密部分集合の要素については,可算であることの witness になっている数え上げでの最小元をとる,という具体的な選択が可能なので,このことを用いると,これらに関する定理の多くは,選択公理なしで証明することができます.例えば,数列を介しての議論の多く (無限個の項を持つので一般には存在の証明で選択公理が必要になることあり) は,ℝ や ℂ での数列を,ℚ や 𝑄 での近似列で置き換えて議論することで選択公理をはずすことができます.
しかし,有界閉集合がコンパクトであること (Heine-Borel の定理) のスタンダードな証明では,このトリックを用いずに証明から選択公理を外すことができます.例えば,
Heine–Borel
theorem - Wikipedia
に書いてある証明 (この記事では,ℝ や ℝⁿ で議論していますが,ℂ での場合も,ここでの証明の変形で証明できます) では,
選択公理が必要に思える議論は,ℝ の単位区間 [0,1] の有限個の区間への分割の列 𝓟ₙ , n
∈ ℕ で,各 n に対し,𝓟ₙ₊₁ が 𝓟ₙ の細分になっているものを選び (これは具体的に取れるので,
選択公理は必要になっていません) 各 n
∈ ℕ に対し,ある条件を満たす 𝑇ₙ ∈ 𝓟ₙ を選んで,𝑇₀ ⊇ 𝑇₁ ⊇ 𝑇₂ ⊇ ··· となるようにする.
という,この最後の 𝑇ₙ たちを (全部いっぺんに) 選ぶところで選択公理が用いられているようにみえます.
しかし,ここでは, 各 𝓟ₙ は単位区間の有限個の区間への分割であることから,ℝ 上の通常の順序 ≤ に関して, 例えば,例えば該当する区間たちのうち,一番左にあるものを取ってくる, というルールで選択することで, 選択公理の使用を避けることができます.ℂ では代数構造と整合性のある全順序はありませんが, 例えば辞書式順序で考えて同じような議論をすることができます.同じ議論で,任意の n ≥ 1 に対する ℝⁿ, ℂⁿ の有界閉集合がコンパクトであることも証明できます.
と書いてみたのだが,この toot を embed するコードで別の html ファイルから引用すると表示が崩れる.
formula は,極力 utf-8 で書いて, 上付き下付きのみを LaTeX に渡すようにした方がよさそうである.その方式で書くと,
となる.これの source code は: { \( r\in ℝ \) : \( r \) は \( \mathsf{L}\) 上の Cohen real }. である. (ただし,MathJax が稼働しださないために,inline math mode の boundary の “backslash parenthesis” を全角の「バックスラッシュ・括弧」 で置き換えている).
[23.01.18(水10:44(JST)) の補筆]: この問題は,その後,解決されている.この toot を書いたときに MathJax の使用を極力避ける工夫を考えたため, その後,utf-8 のコードを効率よく書けるような工夫をすることになり,手元で動いている emacs 上の skk では, たとえば,▽pairof[return] とすると, “〈,〉” が出力され,▽matha[return] ▽mathb[return] で “𝑎 𝑏” が出力される, などという辞書の拡張を行なった結果,〈𝑎, 𝑏 〉 は,utf-8 でストレスなしに書けるようになっている. $\sqrt{n}$ というポストも, そのやりかたで書いたものである. ただし,題字の $\sqrt{n}$ は MathJax を ``$\sqrt{n}$'' として起動させて書いているのだが.
多少は修正が施されている,と言っても,もう二千年以上使い古された democracy を,更に修正する方向に進まなければいけないはずの世界が (Precht はちょっと前に ZDF の彼の番組で Demokratie 2.0 という言い方をしていた),むしろ dictatorship に向ってしまっている, というのは何ということか,とも思うが,種の習性をそう簡単には変えることはできないのだろう.
この dictatorship への移行は,人類の滅亡をかなり早めることになるかもしれない. 人類が,石器時代人として滅ぶ,というのは,僕の望むところでは全くないが,それでも, もし人類が,石器時代人として滅ぶということなら,それはそれで,この種にふさわしい最後, と言えるのかもしれない,とも思う.
ただし,この展開のバリエーションとして,このすぐ先に核戦争が始まって, 近代戦争をする種として,突然に滅んでしまう, という,もう少しましな最後 (?) のシナリオの可能性もないわけではないだろう. それを期待すべきなのか,すべきでないのか ...
ちょっと長くなりそうなので,(tweet の thread でなく) 以下で続けて書かせてください.
本を見ないで, 発言するのは無責任なので,今,『NHK 日本語発音アクセント新辞典』を購入しました. MONOKAKIDO Dictionaries app 内での purchase なので,他の版とは異るかもしれませんが. 本を買ったことで,本を批判的に論じることの権利も十分に得たと理解しています. もちろん,この「批判的は」,critical の意味で「誹謗的」という意味ではありません.
この辞典では,発音は, 高低でなく differential で書いてあるのですね. これは言語学的に確立している記述法なんでしょうか? 日本語,あるいは,少なくとも標準語のアクセントは,differential ではなく高低で機能していると思うので, これでは中途半端な近似になってしまっているような気がするのですが ...
ただし, 「標準語」というのが,ドイツ語の Hochsprache のような完全な体系を目指すものではなくて, 日本語を interregional に話すときの大まかな指針,にすぎないのだったら, 僕がここで言っていることは,「山の手の東京語」についてで, 「標準語」についでではないのかもしれません.また,英語の native speakers が世界共通語の英語にあぐらをかいてしまって, 言葉をみがけないでいることが多いのと同じように, 自分が話している日本語が,巷で 「標準語」と言われる日本語に限りなく近いことに,あぐらをかいてしまってしないか, 十分に注意して書いてはいるつもりですが,不注意な点があったらごめんなさい.
僕が, 前の tweet で言いたかったのは, 橋,端,箸の pitch accent の区別がされているかどうか,ではなくて,pitch accent が単語よりもっと大きなまとまりで機能しているし,この機能は differential ではなく高低で機能していて,しかも accent のつけかたが同じ文言で複数可能な場合もあるし, その場合には semantics に踏み込んだ区別が必要だし,そういう区別についても, 方言による違いがありえるので,ガイドラインとしての標準語だとしても, 用法の統一が必要ではないか,ということです. この本はそういう議論を全部ぬかして pragmatic なガイドに徹しているように見えるのが,気になるのです. 日本の文化が言葉をないがしろにする傾向にあることに日頃腹をたてているので, 八つ当たり気味になってしまっているかもいれません.そうだったらごめんなさい.
この本の 『おすすめポイント』 で cite されている,「男の子」の例で言うと,
「男の子がいます」.は,
_o_ ‾to‾ ‾ko‾_no_ _ko_ _ga_ _i_ ‾ma‾ s(u)
_o_ ‾to‾ ‾ko‾_no_ _ko_ ‾ga‾ _i_ ‾ma‾ s(u)
の二種類の発音が可能で,意味としては,二番目のものの「男の子」に,の subject marker がより強くかかるものになる,という区別があると思います.
一方,橋,端,箸のように助詞こみで区別をすようになっている単語では, 同じような pitch での区別をすることができなくて,stress での区別をすることになります.
この例は, pitch accent が differential でなく高低で機能していることの例証の一つになっていると言えるのではないかと思います. (東京以東,以北の言葉にはあまり詳しくないので,間違っているかもしれませんが) 東京以東,の言葉の中には,この区別がなかったり逆になったりするものがあると思います.
[この項は,まだ書きかけです]
“湯川・朝永” は,結構長い期間,日本でロールモデルとして機能していたと思います. 湯川先生がノーベル賞をとったのは1940年代ですが,1960年代,小学校6年生が対象の 「科学教室」という東京の(当時,北多摩と呼ばれていた) 地区の各週に開催された特別授業の発表会で, 司会をした先生が 「発表者のうちの湯川君は, 将来は湯川博士になるのでしょうが ...」というスピーチをしたのを覚えています (ちなみに, このとき小学6年生だった僕も,毛細管現象と表面張力の関係に関する処女論文を発表しています.).
湯川先生といえば,Feynman の "You are kidding ..." に,日本語では,「私がディラック方程式を解きました」と言う時と, 「湯川先生がディラック方程式を解かれました」というときと別の動詞形を使うことを知って憤慨して日本語の勉強を やめた,という逸話が書いてありました."Surely, You are kidding Mr. Feynman" は, 1985年に出版されています. 僕は,逆に,敬語は,色々誤用して遊んだり, 間違って使った人をおちょくったりできるので,面白いとも思うのですが.
スーパーコンピュータに関しても, 「富嶽は現代の Stonehenge である」というのは有意な命題と言っていいだろう.「日本の新聞」に, 「富嶽が ... を検証しました」というような記事が出ているのを見るたびに, このことを考えてしまう.
旧石器時代人を説得するのに,古代スーパーコンピュータStonehenge は,大変な効果を発揮したのだろうから, 最新のストーンヘンジとしての富嶽の権威で(新)石器時代人を言いくるめることが容易である, ということは十分に想像ができるのだが.
--- 西脇順三郎,『キャサリン』,『近代の寓話』(1953) に収録.
メールで,「すう゛ぁらしい!」 と書いてから,これを思い出した.
‘=’ には,
① (a) 同一性,または,(b) 同等性を表わす記号,
② 代入の操作を表わす記号,
③ 定義を表わす記号
などとしての異る解釈があります.どの意味で使われているかは,多くの場合明示されず, 読む人が文脈から読みとることが求められていることも少なくないようです. コンピュータ言語では, ① と ② の ‘=’ を区別するために,① の ‘=’ を ‘==’ と書くことになっているものや, ② の ‘=’ を ‘:=’ と書くことになっているものもあります.③ の ‘=’ も, ① のものと区別するために,‘:=’ や ‘≝’ などと書くこともあり,日本では,‘≜’ という記号が使われることもあります.
A=B と B=C が成り立つなら A=C である は推移律 (transitivity) と呼ばれる“法則”です.
既に解答している方の解答には,② の代入記号としての ‘=’ について論じているものがありますが, 推移律が問題になるのは,① の意味の ‘=’ です.以下で,これについての, 説明を試みたいと思いますが,① のうち,“(a) 同一性” は,哲学的な問題と見ても, 物理学の問題と見ても,非常に難しいものを含んでいて,ここで議論しきれそうにないので, “(b) 同等性” を表わす記号としての ‘=’ についての説明をしようと思います.
論理学の立場からは, 同等性の推移律は,同等性が満たすべき基本性質 (公理) の一つとして導入されるのですが, 質問は,なぜこの公理が導入されることが妥当なのか,ということでしょう.以下はその説明です. 二つの (概念や具体的な物や人や生きものなどを含む) 対象が,同等である,とは, この二つがどんな性質によっても区別できないこと, とします.例えば,同等な人物が同時に二つの場所に現れることはありません. もしそういうことがあれば,「何時何分にこれこれの場所にいる」という性質で区別できるので, これらの二人の人物は同等でない, ということになってしまうからです.つまりドッペルゲンガーたちは互いに同等ではありません.
今,A と B が同等で,B と C も同等だとすると,任意の性質 𝓟 に対し,A は𝓟 を満たす <=> B は𝓟 を満たす,また,B は𝓟 を満たす <=> C は𝓟 を満たす,が成り立ちます.(“<=>” は, 二つの命題の論理的な同値性を表わす記号です) したがって,このことと,論理学の法則 (あるいは, “<=>” のここで言ったような解釈の定義) から, A は𝓟 を満たす <=> C は𝓟 を満たす が成り立つことが帰結できます.ここで 𝓟 は任意だったので, A と C が同等だということが証明できたことになります.
同一性は,哲学的または物理学的に難しい概念だと言いましたが, 同等性も実は上で書いたことを分析してみると,結構微妙な問題を抱えていることがわかります. たとえば,A と B が同等であることを確かめるためには,すべての性質𝓟 について,A が𝓟 を満たすことと, B が𝓟 を満たすこととが同値であることを確かめなければならなくなるわけですが, そのような性質は無限にあるかもしれないので,その場合には, これを確かめることが不可能になってしまいます.このような問題について議論を始めると, とても長くなってしまうので,ここでは問題を指摘することにとどめておくことにします.
ドイツやアメリカには「おフランス」(つまり,フランス文化は高級,という価値観)があった (今でも残っている?— たとえば20世紀前半のパリはアメリカの金持ちや文化人であふれていたし, たとえばナチスドイツがパリを占領したときも,占領政策は,占領した他の国に比べれば (あくまで比較の問題ですが)ずっと人道的なものだったのは, このフランス文化は高級というドイツでの価値観が影響していたのではないかと想像します)ので, 日本の昔の 「おフランス」は, 20世紀前半での,この価値観のドイツやアメリカからの輸入という面があったのではないかと想像します. イヤミ氏の「シェー」は,ドイツ語の „schön!“ (英語の "good!" に対応する表現) から来ている, という説を聞いたこともあります. —- おそ松くんやその前の時代だけでなく,今でも schön を連発する年配のドイツ人は少なくないと思いますが,実際,これを真似して schön を連発するヨーロッパかぶれの日本人の人物が,当時のおそ松くんの作者の周りにいた, というような説明を読んだ気がします.これは十分にありそうなことに思えます.
英語では,日本語で「ミーざます」というのと同じ具合には me という語形を使わないので (”it's me” と言うことはできるかもしれませんが, これは „schön!“ や "good!" のように自然に連発できる表現ではないでしょう), 「ミー」というのは, 「ヨーロッパ系外国語なまりの日本語」に対する日本でのステレオタイプにすぎないのではないでしょうか. ちなみに,倉本聰脚本の「波の盆」 (1983) で,在りし日の笠智衆の演じている日系ハワイ人が, 「ミー」を連発するのは, すごく残念な気がします.このテレビ映画につけられた武満徹の音楽のファンとしては, 本物のハワイの日系一世の老人の話す日本語を,リサーチして台本が書けていたらよかったのにと思ってしまいます. ( とは言っても, ごろうさんの北海道語は, このハワイの日系老人の日本語よりずっと精度が高いような印象を受けるのですが.)
「ミー」に関する憶測をもう一つ加えさせてください. 英語で “me” (ドイツ語では „mir“ または „mich“) と単独に言うことはなくても,“for me” (ドイツ語では „für mich“ — 「私にとっては 」) を連発する癖のある人なら結構いるかもしれません. 日本人は,語尾の子音や, 飲み込んで発音された,殆ど子音だけしか聞こえなくなっている音節を全く聞き取れないことが多いので, これを「ミー」と聞き取って,『外国人は「ミー」を連発する』と理解した, というのは,説得力のある説明のように思えるのですが,どうでしょう?
更にこれを真似て「ミー」と日本語で言うというのは,どうかとは思いますが,もし, イヤミ氏が,まさにそういう経緯で「ミー」と言っているのだったら, これはもう (ドイツ語のもともとの意味で,皮肉を込めて) 「シェ〜っ」と答えるしかありません.
終ったときから始まる 秘められた夢の旅 たとえば船室のような部屋に 飾られた一枚の海図 それらが揺らめいて 光りに映える水面となるとき 笑いさざめくエーゲ海の まぶしい朝の中にいる --- 新倉俊一 『ビザンチュームへの旅』(2021) の始めは,武満徹の思い出に捧げられた,Sir Simon Rattle の
Colorの終わりの sequences の映像を連想させる.
Rattle は,この音楽番組/ドキュメンタリー(?)で,武満の Dream Window の, Rattle 自身の指揮による演奏を背景に, 武満の音楽について,音楽の色彩について,東と西の融合について,語っている.Dream Window は夢窓国師で,武満の語る庭園の回遊の音楽の視覚化となっているタイトルでもあるが, 言葉通りには「夢への窓」でもある. Rattle のフィルムの映像は, Dream Window の最後の和音魂が消えさってゆくのを背景に (音楽家の作ったフィルムだから, 音楽が途中で無神経にプッツリと切れたりはしない) 「船室のような部屋に飾られた」画額たちに, このドキュメンタリーでそれまでに紹介された音楽の背景となっていた映像たちが,ゆらぎならが投影されて終る.
18世紀の Ombres Errantes は燭台の光りにゆらぐ影たちだったが,20世紀末の Ombres は,コンピュータグラフィックスのアルゴリズムの影にゆらいでいる.
詩集の巻頭を飾るのは,
本の題名ともなっている,『ビザンチュームへの旅』という題の,旅と東西のローマにまつわる二行連詩である.
「ビザンチュームへの旅」は,今は,トルコ民族に征服されてイスタンブールになってしまった,
ビザンツの面影を残す,ハギア・ソフィアへの旅だが,他の詩 (『冬の旅』の中の『ボン ナターレ』) では,
この「大伽藍」について,
「今はモスクとなって/拝観はできないそうだ」と Erdoğan
大統領の2018年の措置が歌いこまれている (この,
突然,同時代の政治/風俗を timeless
な詩の世界に投げこむ,というのも,西脇順三郎が屡々用いる手法である).
詩の中では,Ambarvalia の『皿』が何か所かで引用されているが,僕は,
昔,「黄色いすみれの咲くころの昔」と題した,エルサレムに住んだときのことを書いた作文
のエピグラフに,この詩を引用したことがあった.
詩はかつての東西のローマに思いをはせるが,
何が現実地理上の旅で,何がラテン語の夢なのか判別できない (後の『めぐりあい』という詩では,
須賀敦子の紹介で若いイタリア人の先生にラテン語を習ったことが書かれている).
ビザンチンを模したイタリアのサンヴィターレ寺院に言及した後,旅人はこの伽藍をも後に旅を続けるが,
「サン・ヴィターレを出て/明日はまた新しい旅へ」この何気ないように見える詩行も,西脇順三郎の
「明日はまた新しい野原へ ---」(『北海の旅』,『醸』など) を透して,Milton の, To-morrow
to fresh woods,
and pastures new.
に繋がってみえる.旅人が去った後も,この聖都の幻影は残っているのに,
我々の視界の前には,それとは違う位相の現実の世界が,当然のように,横たわる
そとでは相変わらず波が映え 街はまだ喧騒に満ちているが --- 新倉俊一 『ビザンチュームへの旅』(2021) 最終行

Będlewo にあった楽器も, こちらはアップライトだが,やっぱりこんな感じのピアノのお稽古的な楽器だったのを思い出した. このニューヨークのスタインウエイは,いい音はでてはいるし,調律も442だったので, 風呂場で歌っていい気分になるようなノリで,楽しく弾いてしまったのだが ...
日本語版 Wikipedia で見ると, この日本語訳は,1927年から,1945年の間と,1952年から,1985年の間に教科書に採用された, ということである.前者の期間は, 日本が,統治していたアジアの国々で日本語教育を強要していた時期と重なっているし, 後者は,前者の時期に対する反省を拒否していた時期と重なっているわけなので, いずれにしても,意図が計りかねる.そうずっと思っていたのだが,今日, 起きて考えたら,整合的な説明になりそうな,見方に気がついた.
1927年から1945年の間の期間については, 朝鮮半島を含むアジアのいくつかの地域を統治していた時期の日本の平均的な日本人の意識や, 為政者が平均的な日本人に植えつけたいと思っていた意識については, 調査不足だし,ここでは言及しないことにしたいが,1952年から,1985年の間については, 特に,1952年からのこの期間の最初の方については, 1952年が連合国からの占領のステータスを脱却した年なので (この4月に被占領国のステータスを抜け出ている), やっと言いたいことが言えるようになったタイミングということなのだろうが, そこで言いたかったことは,もちろん日本がアジアで日本語教育を強要したことの謝罪ではなく, むしろ,文化政策的の結果による英語化での日本語の消滅に対する危機感ではなかっただろうか.
ただし, 日本での英語教育の壊滅的な負の成果は,この危機感からの,努力の結果,と見るべきか, 平均的な日本人の言語能力の低さの当然の帰結と見るべきかは,よく分らない気がする. 多分,この両方なのだろうが ...
しかし, このストーリーが示唆しているような,複数の言語を,同時に普通にきちんと使いこなすことへの否定に歩みを進めてしまったことで, 日本は,方言は話せるが, 日本語は話せないという日本人を大量生産してしまう,という道を突き進むことになってしまったのだと思う.
私は煙草のアレルギーがあるおかげで, 歩き煙草をしている人の周りにどういうふうな煙草の煙の雲ができているかをよく知っている. 道で,歩きたばこをしている人とすれ違うときには, その煙の雲のただよっている範囲と思われる場所を歩いている間息をとめていたのだが (これは相当長い時間になる, また,喫煙者が前を歩いているときには,息をとめて走って追いぬく), covid-19 が流行しだしてからは,すれ違ったり,近くを歩いていたりする人が, 歩行喫煙者であるかどうかに拘わらず, この煙の雲の範囲 (これは, 煙草を含んでいたとしたらその臭いやそれに含まれるアレルゲンが気になるであろう濃度の排気の存在している範囲, と考えていいだろうし,もし排気にヴィルスが含まれていたとしたら, それが感染を起こすかもしれない濃度の範囲であることの目安と考えてもいいだろう) に入っていると思われるところで, 息をとめたり,息をとめて走って追いぬいたり,ということをマスクの下でしている.
何かの数学的な議論の途上で, 各自然数 i ∈ ℕ に対し,実数の空でない集合 Rᵢ ⊆ ℝ が与えられているとします. このとき,すべての i ∈ ℕ に対し,rᵢ ∈ Rᵢ が成り立つような実数の列 〈rᵢ: i ∈ ℕ 〉 を (いっぺんに) とることができるでしょうか? このようなことがいつでもできる, ということの保証を与えるのが選択公理です.ただし,選択公理は,添字が自然数の全体以外でも, 各 Rᵢ も (必ずしも ℝ の部分集合でない) 任意の空でない集合の場合でも, このような列がいっぺんにとれることを主張するものになっています.
たとえば,各 Rᵢ が すべての実数の集合 ℝ の部分集合ではなくて, すべての有理数の集合 ℚ の部分集合だったとしたら, ℚ の要素は, q₁, q₂, q₃ ,... と一列に並べることができるので,この場合には,たとえば,Rᵢ の要素のうち, この並べあげに関して最小のものをとる, という規則に従って,〈rᵢ: ᵢ ∈ ℕ 〉 を (いっぺんに) とることができます. したがって,この場合には, 選択公理なしで,数列を選んでくることができます.でも,(Rᵢ ⊆ ℝ の場合を含む) 一般の場合には, 必ずしもそうとは限らないことが証明できるので (この証明はかなり難しいものです) , 選択公理は通常の数学の議論で実際に必要です.
ちなみに,選択公理が必要になる数学的な局面は, (例えば大学の一年生が一般科目として習う (初等的な) 数学の範囲でも) それほど多くはないですが, いくつかは存在します. たとえば,初等数学ノート の 「関数 (の値) の収束と選択公理」という題の節 を参照してみてください.
ハウスドルフの場合は,そもそも,問題となっていたのは,言論の自由ですらなく, 尊厳の保持や,生存の権利だったのだが, そのような国を去る決断を先延ばしにしていると,死に追い詰められることだってありえる.
Endenich は Endenich (終りでない) ですらない(*).シューマンは Endenich で生涯を終えたが, ハウスドルフは,Endenich で不名誉な死出の旅に就くことを拒否して自害した.
(*) ハウスドルフは, 1942年に強制収容所への輸送のための集合収容所だった Endenich への招聘を受けた後, 自害を決意して,友人にあてた遺品の処理を請うている最期の手紙に,„Auch Endenich Ist noch vielleicht das Ende nich! Was in den letzten Monaten gegen die Juden geschehen ist, erweckt begründete Angst, dass man uns einen für uns erträglichen Zustand nicht mehr erleben lassen wird.“ と書いている.
ついでに言えば,ドイツだって Graf von Stauffenberg 大佐にもかかわらず,ドイツが無条件降伏したのは,首都が,ほぼ完全に物理的に破壊された後だった. 東京のように焼け野原にならなかったのは,家が石造りだったからで,大量の瓦礫は, 山 (というか丘) になっていて, 今では,ZDF のベルリン支局からのニュースの背景になっている (Teufelsberg がそれである. 山頂に立っている冷戦時代のアメリカ軍のレーダー施設の廃墟が何ものかを象徴している.) .
この映画の中で,昔のことを色々と思い出している, 初老にさしかかった主人公が,固くなった体をまげて難儀に上着のシャツを着るシーンがあって, これを見たときには,自分とは関係のないことと思っていたが, 今,固くなった体をまげてやっとのことで服の中に体を押しこむときに, いつもこのシーンを思い出してしまう.
twitter が tweets の(一度消して書きなおすことでしか) 推敲を許さない, というのは,twitter を,言いっぱなしではなく,思索の道具として使いたいときの, 大きな障害になる.もとの tweets を消さなくても,推敲の履歴をネットに残す形で, 訂正を許すようにしてもらえないだろうか.
oxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxox
ところで高瀬さんは「フェルマ」と書かれるんですか?フランス語では, 最後のシラブルにアクセントがあって, pitch accent ではないにしても,音が少し上がり気味になるので, 確かにこの書き方の方が,カタカナ読みで原音に近くなるかもしれないですね. フランスの近代の作曲家で,Gabriel Fauré という人がいるんですが,この名前は, 日本語では,ガブリエル・フォーレと書かれることが多くて, 日本人がこのカタカナ読みをしたときに,ヨーロッパでは絶対に通じません. ちなみに,僕自身は, カタカナ読みをしても通じる可能性のある,「ガブリエル・フォレー」という表記を使って, 発音するときにはフランス語に近い発音やアクセントで言うようにしています.
--- 「現地で確認済み」というのは,なんの保証にもならないと思います.2つ反例があります.
反例 その1. 画家のミロは,スペインのフランコ独裁政権 (カタルニアで, かつて日本が沖縄や植民地でやったような ひどい 言語政策をしていました) の時には, スペイン語読みのホアン・ミロと表記されていましたが, 今では,カタルニア語読みのジョアン・ミロに訂正されています.もし,保守的なスペイン人の "現地の人" に聞いたら「本当はホアン・ミロが正しい」と言うかもしれません.
反例 その2. ヒルベルトの有名な „Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können“ は古い (擬古文調の) ドイツ語の文語表現で言っているので, 学校ドイツ語語の文法では間違っているように,見えます.ドイツ人でも 「ちはやふる」の人がいるので, 間違っていると言うかもしれません.実際,「ドイツ人から聞いたが,間違っているということだった」, と書いた日本人の作文をどこかで見たことがあります.
Bernoulli は,僕の 学問的祖先 なので (Johann とJacob が家系図に挙げられています),正しいところを知っておきたいです. 生地のバーゼルは歴史的に三カ国国籍なので, ミロの例のように, フランス語圏の現地の人に聞くか,ドイツ語圏の現地の人 (といってもスイスドイツ語は, ドイツ語とは別の複数の言語です) に聞くか (また, 聞かれた人に教養があるかないか) などで,答えが違ってくると思います. ちなみに,フランス語風の発音でも "ll" は発音されますが, 日本人の耳には "ヌ" と "イ" の間の分離としてしか聞こえない可能性があります.
例えば,現代ドイツでは,ポーランドの苗字を持っている人でも ドイツ語風の発音で名乗っている人もいたりするのですが,Bernoulli は名家なので, これとは似たような例には,なっていような気がします.ただし, Bernoulli はフランス系の家名 (先祖はアントワープから来ているようです) です. ドイツでは,逆に,フランス風の家名の発音を保持している家もあります. 例: Thomas de Maiziére (1954 --): ドイツの政治家で,祖先は(ベルリンに移住した)ユグノーということです. "教養のある" ドイツ人は, こういう名前を発音するときには, これみよがしに,ドイツ語にない,フランス語の音の "é" とか "r" で発音します. さすが,日本文化での,「おフランス」の発祥の地です.
… というようなことも含めて,「現地で確認済み」は, クワインの Gavagai みたいで, すごく面白いですね.
今ネットに転がっていた音声データをいろいろ聴き比べてみて考えてみたのですがベルヌーイもベルヌリも問題はむしろ 「ル」の方のような気がします. ベㇽヌㇼイはどうでしょう? これだと, ヨーロッパ語の可能な発音の平均(でもないか) に近いものになるような気がします. Cantor も慣習でカントルと書いていますが,個人的にはカントㇽと書きたいです.
ドイツ語で Cantor と発音した時には日本語が母国語の人には,カントルよりカントに近く聞こえると思うのですが,哲学者のカントの方は (この人も僕の祖先です) これをカンㇳと書くことで, 上手く表記ができます.
--- 『西欧語のカタカナ表記は幕末+明治初期から今日まで悲喜こもごもの有為転変の経緯がある』, というのは僕もそう思います.ポトガラヒーもビルヂングも捨てがたいし, ギョエテとは俺のことかとも思ってしまいます.しかし,日本語に対する愛おしさとは別に, 日本語を捨てるべきではないかとも,常々思ってもいます. また,先人に敬意は,先人のやったことを死守することで,表されるというより, 自由に改良して, 必要なら,更に,historical remark を添えて,どのような形の貢献を,誰がしたかを銘記することで,表されることになるのではないでしょうか?
► 以下は,tweet するのがだんだん億劫になってきたので,直接, ここに書くことにしています.
日本語を捨てる,と言っても,できることなら書き言葉は捨てないですませれば, とは思っています.日本語の話言葉は (もし書き言葉と分離できるなら) 捨てていいと思います. 過去にもラテン語のような,話言葉を捨てた言語はあるので,これは不可能ではないと思います.
日本語への transliteration の話に戻ると,統一した transliteration の体系があるのは, 例えば自動翻訳などのためには,都合が良いのでしょうが,個人的には,それ以外では, 特に全体として統一しなくてもいいのではないか,と思っています.それより, もっと重要なのは,日本語の文語に, アルファベットの単語を (アルファベットのまま,かつ元の発音のまま) 統合することを,推し進めることだと思っています. アルファベットとしては,最低でも (可能な diacritics をすべて含んだ) ラテン文字でもいいのかもしれませんが, 他のアルファベットも必要なら導入してよいでしょう. 日本文化が 1500年か1600年前かに中国の文字を受け入れたのと同じような意味で, アルファベットを追加で受け入れればいいのではないでしょうか.そうすることで, たとえばベㇽヌㇼイと書かずに Bernoulli と書くこともできますし Tchaikovsky になったり, Tchaikowski になったり, Tchaïkovski になったりせずに, Чайковский と一意に書くこともできます.これも,別に一意にオリジナルの表記だけを許す必要はなくて, 日本の西洋数学の受容の歴史を論じている文脈では「ベルヌーイ」とすればよいし, フランスの近代でのロシア音楽の受容の歴史を論じている文脈では, «Tchaïkovski» とすればよいでしょう.昔なら,これは, あまり現実的な提案ではなかったかもしれませんが,現代では,我々の知性は, コンピュータやネットワークで補強されているので,十分に妥当な提案だと思います.
日本語は,語彙がその本質なのではなく,本質的なのは,その膠着言語としての文法の核でしょう. こう見ると韓国語と日本語はほとんど同じ言語と考えることもできるような気がします. この膠着言語としての文法の核の特性を生かして, 言語の phonetical system を大胆に拡張して (これも音声データをネットワークからダウンロードして聴くことのできる現代では, 昔とは全く違った意味で実現可能になっていると言えると思います) 国際語となっている言語の語彙や文法要素を, そのまま,日本語に積極的に統合することで, 日本語自身を, 日本語として最大に生かせるし (かつて, 日本語と現代の韓国語のもとになった言語が語彙を急速に入れ換えて袂を分けることになったのも, この両言語の文法構造の核の特性に起因するものだったのではないでしょうか?), 非常に手っ取り早く, 日本語を国際語にすることもできます.上で,日本語を捨てるべきではないかとも, 常々思ってもいます, と書きましたが,日本語の書き言葉の, このような展開が可能なら,僕自身も,少なくとも 日本語の文語は,捨てなくてもいいのではないかとも思っています.
僕が日本語の口語は捨てたいと思っていることの背景は, 他のところでも何度も書いたことがあると思いますが, 一番の理由は, 日本語が,この言語での対話が成立するためには, 話者の間の上下関係が決定されることが必要であるような仕組になっていることです. この設定が, 言語に組み込まれているのか,社会に組み込まれているのかは微妙なところでもありますが, 日本語にも韓国語にも敬語がある, という事実は,これが,社会に,というよりは,言語に組み込まれた設定である, と考えることが妥当であることを示唆しているように思えます. もちろん,上下関係を決めることが会話の前提となっているかどうか,とは別に, どこでも mansplain したがる奴や,(より日本語的な表現で言うと) マウントをとりたがる奴はいるし, 無意味に下手に出て,おべっかを使って得をしようとする奴もいるわけですが, 言語の枠組が,話者の関係の非対称性をデフォルトで,更に助長することが, (少なくとも内容をともなったコミニケーションの手段としては) 良いことであるはずはありません.
[この項はまだ書き足す可能性があります]
Even after the Incompleteness Theorem, one could still consider the impossibility of such work model as merely theoretical. But, at the latest, since Gödel's work on constructible universe, it should be clear that set theory can only be full-fledged when logical and mathematical parts of the theory are united.
Hausdorff was forced to leave this world of research in 1942 (when he killed himself togeher with his family, after the order was given to them to show up in the „Sammellager“ in Endenich the place where Robert Schumann died in a "hospital" half a century ago --- as a music expert, Hausdorff must have been aware of this connotation). Thus he could not see the development of the set theory after Gödel's red book (which was published in 1940 in the United States).
Some people say, Hausdorff in 1930s was too old to see what was done by Gödel. But I wonder, if Hausdorff could live into 1940's (in an alternative history), perhaps he had a chance to recognize this inevitable unity and corrected his attitude and/or his text books in his very high age.
かつての社会主義国家の「書記長」のように, どんなにシステムや役職を設定しても,その役職についた人も,その回りにいる人も,これが 「権力者」なのだと誤解してしまう,という古代性の茶番は,日本人に限らないし, 為政者を叱責して,本当に殺してしまったりする文化もあるので, 日本は,それよりはましとも言えるかもしれないが… .
[1] 渕野 昌, 初等数学ノート,1.11 関数 (の値) の収束と選択公理
Outside the model $M$, that is, in the true set-theoretic universe, where $M$ is merely a set, they do know what $Th(M)$ is, namely $Th(M)=\{\varphi:\,M\models\varphi\}$, and so the truth of our world $M$. On the other hand, they do not know their truth, at least not as a knowledge in form of a single formula, because of Tarski's theorem.
Awakened from this mathematical dream, we are sitting in a cool room of meta-mathematics. Here, we have no absolute infinity but an infinitely wide paper and infinite time to write mathematical proofs on it. There is nothing like "the truth" but we have a concretely given axiom system like ${\sf ZFC}$ $+$ "there exist class many superhuge cardinals" and can appreciate all the theorems we could deduce form this divine axiom system, and these theorems are our truth.
There is still a world outside this confinement of what we consider as divine mathematical game of proofs. In the outside world they contemplate about all possible axiom systems and discuss if the axiom systems are consistent, or at least reasonable, and if they are in a position at all to be able to discuss such things like the consistency.
◆ 間違えて,fifth wave と書いてしまっているが,ドイツではまだ fourth wave である.日本と波長が違うようなのは不思議が,沢山の国が国境でつながっているヨーロッパと, 「水際」がほとんど空港に限られている (本当にそうなのだろうか?) 日本との違い, ということなのかもしれない.
この,„Der Kommissar“ に関しては,der Kommisser Keller と部下の関係 (全員 Biodeutsche
で,straight で,秘書の女性たちを除くと,
全員男性である --- これは現代のドイツの刑事物では,あり得ない) は,
現代の日本の人間関係に似ているように思える.
文化の違いと理解されることの多くは,実は,単に時差の組合せにすぎないのではないか.
背景で Gastarbeiter が色々な言葉 (主にイタリア語) でしゃべっているシーンが出てくる.
これは現代日本だったら,新大久保の街角のシーンかなにかが挿入されるようなものだろう.
もちろん,連絡は全部 (固定) 電話である.
スマホ (ドイツ語ではHandy) がないだけで,こんなにも話の流れの連続性が,
違ってくるものなのだとは思わなかった.
電話ボックスの他,ホテルのフロントや,バーのカウンターのシーンが沢山出てくるが,
それは,そこに電話機があるからである.
現代のドイツの刑事物との,もう一つの大きなちがいは,登場人物の多く,特に男性成人のほとんど全員が,
チェイン・スモーカーであることである.画面はタバコの煙で充満している.
ときどき「煙草を吸っていいですか」という台詞が挿入されるが,誰も „Nein“ とは言わない.
もっとも,現代のドイツの刑事物でも,刑事たちが非喫煙者であるとは限らなくて,特に,
高齢者の視聴者を対象にしていると思われるシリーズでは,危機が去ったときに,屋外の喫煙所で皆で煙草をすう,
などというシーンが,挿入されたりさえ,するのだが.
この喫煙シーンの変遷で改めて思ったのは,人類は,合法麻薬の一つを (ほとんど) 卒業するだけにも,
半世紀以上を要したのに,これから先たった数十年で脱炭素化を成し遂げて,
絶滅を回避できるはずがない,ということだった.
「環境問題」に関連する社会へのプロテストとして,
自動車の免許は一生とらない,と決断したのは,僕が学生だったころの1970年代だった (Der
Kommissar とほとんど同時期である --- これは今も守っている.
もっとも,将来アメリカに移民することになったとすると,
生活上の都合から,この決断をやむを得ず破らなくてはならなくなる可能性もなくはないかもしれない) が,
それから半世紀近くたった現代でも,自動車は,未だに世界中に蔓延っている,
自家用車の自動車総数に対する比率は,明らかに,当時より,
更にずっと高いものにすらなっている.
自動車などの内燃機関や,火力発電所などの火力施設のエネルギー効率は,現代にいたる改良で,
飛躍的に上がっているに違いないが (昔は,
この改良の可能性が,何も手段を講じないことの言い訳の一つだったと思うし,
ネットを見ていると,今でも同様の勘違いをしている人たちが多数いる),
二酸化炭素の総排出量で見れば明らかなように,
総量は,エネルギー効率の改良を相殺して余りある (もちろん何もしていなかったら,
もっとひどいことになっていたはずなので,
エネルギー効率の改良が全く無意味だったとは言えないかもしれないが,
商売として成り立っている限り,効率が良くなれば,需要ものびなければいけないので,
文明自身が変らないかぎり,解決とは反対の方向に行ってしまうことも確かだろう).
東ドイツ人が西と統合したがったのは,
西の車が欲しかったからに過ぎなかったと言えるように思えるが,
これは自動車と,人類の本能との関係を説明するための好事例になっているように思える.
現代では電気自動車について議論されることが多いが,
電気自動車が,解決でなく,ごく短期間に対しての過渡的な時間稼ぎに過ぎないことは,殆ど誰も理解していないように思える.
しかも,上で言ったような総量の相殺の効果から,これが何か有意義な事態の改善につながるかどうかさえ怪しい.
結局のところ,これは,単に良心の呵責から逃げるための言い訳になるにすぎないのではないか.
しかし,良心の呵責から逃げるための言い訳を持つことは,
事態の改善につながらないだけではなく,
むしろ改悪の主要因にもなりえる,ということは,過去の歴史が既に証明していることのようにも思える.
... 回避不可能な人類の滅亡は, 既に,疾うの昔に回避不可能なものとしてプログラムされてしまっている.なぜ,こんな明白な事実に, 誰も気づかないのか.
もちろん,上の (2) には,これ以外にも,次の命題が (真または偽) であることを示せ, とも読めるという問題を含んでいて,そう解釈すると,(真または偽) はトートロジーなので, 命題が well-formulated な限り常に成り立つ,とも言えてしまう,という問題があって, tweet で言っているのはむしろ,この点なのでしょう.
これについては, この tweet の retweets や quoted retweets では, 不完全性定理について言及しているものが沢山ありましたが, 自分がおく理解していないことや, (単なる)未解決問題や,本当に (ある数学体系から) 独立であることが証明されている命題を, 全部一緒くたにして,「不完全性定理現象」とか言うのはやめてほしいものです.
「やめてほしいです」というような言い方をすると, 「なにをえらそうな!」と思う読者もいるかもしれませんが, 僕自身は,不完全性定理に関連する研究を真摯に行なっているし, こういうことを言える程度の研究成果も十分に挙げているつもりです.
この入試問題との関連では,「$n^2+n+41$ が素数でないような $n$ が無限に存在する」は, 比較的簡単に証明できる命題ですが (以下の 「おまけ」を参照),「$n^2+n+41$ が素数となるような $n$ が無限に存在する」は,Bunyakovsky conjectureと呼ばれる仮説と関連するもので,多分,未解決の問題です. (ここでのふたつの命題は,互いに他の否定になっていないことに注意してください.) そうだとすると,この最後の命題で,不完全性定理現象が生じているかもしれない可能性は, 今のところゼロでない,ということになるわけなのですが ... 🚧 この項目はまだ書きかけです 🚧
おまけ:
定理 (Legendre). 任意の,constant でない多項式 $P(x)$ に対し,$P(n)$ が素数でないような $n\in\mathbb{N}$ が存在する.更に,このとき,$P(n)$ が素数でないような $n\in\mathbb{N}$ は,無限個存在する.
証明.
すべての $n\in\mathbb{N}$ に対し,$P(n)$ が素数でないなら,主張は明らかに成り立つから,
ある $n^*\in\mathbb{N}$ に対し,素数 $p$ で,$P(n^*)=p$ となるものが存在するとしてよい.
$P$ は constant でないので,$\lim_{n\rightarrow\infty}|P(n)|=\infty$ である.
したがって十分に大きな,すべての $n\in\mathbb{N}$ に対して,$|P(n^*+np)|>p$ である.
もし $P(n^*+np)\not>1$ なら,
$P(n^*+np)$ はいずれにしても素数ではないから,$P(n^*+np)>p$ としてよい.
このとき,$P(n^*+np)\equiv
P(n^*)\equiv 0$ $mod\ p$ だから.$P(n^*+np)$ は $p$ の倍数となり,素数でない.□
もちろん,これは偶然の一致でしかあり得ないが,この一連の記事を書いた直後に, こんな tweets の string が reocommend された:
しかし,このパンデミックで起っていることは,人類がその終焉に際して如何に果敢に戦うことになるか, ということの示唆にもなっているようにも思える.これは僕にしてはちょっと optimistic すぎるコメントかもしれないが.と書いたが,こういうのを見ると,この optimistic すぎる optimism は折れてしまいそうな気分になりがちである.
Suppose that $\varphi$ is an open problem in the theory $T$ which is waiting a positive solution, that is $T\vdash\varphi$ but we do not know this yet.
Now let $\varphi^*:=\varphi\land\psi$. $\varphi^*$ is equivalent to $\varphi$ over $T$. That is, $T\vdash\ \varphi\leftrightarrow\varphi^*$. In particular, if $T$ proves $\varphi$ then $T$ also proves $\varphi^*$. However, a proof of $\psi$ can be created from a proof $P$ of $\varphi^*$ by attaching a couple of proof steps to $P$. Thus the shortest proof of $\varphi^*$ is also beyond any measure of feasibility.
This example suggests that any mathematical problem can be formulated in such a bad manner that, even if the problem is (theoretically) solvable, it needs a speed-up by moving to a theory which is consistency-wise stronger than the original $T$ to obtain a proof of feasible length.
In connection with the main argument of [1], the discussion above should be a strong support for the non-constructivist approaches in which mathematics is done (also) in a framework far beyond a minimal theory which should be enough for everything in the "applicable" mathematics.
I just realized the argument above with $\varphi^*$ after reading Joel's tweet and his MathOverflow post:
The present entry is also connected to this thread of tweets:
[1] 渕野 昌,数学と集合論 --- ゲーデルの加速定理の視点からの考察 (Mathematics and set theory --- a perspective from Gödel's Speedup Theorem) 科学基礎論研究,Vol.46, No.1 (2018), 33--47.
この人は,どんな危険な民族主義の思想の持ち主なのだろうか.あるいは, 民族主義を完全に超越しているのか.この人が, 「ポーランドのギュンター・グラス」とか, 「中国の朝丘ルリ子」とか,言うのかどうかは,大変に興味がある.
「... 次にカントールは、無理数 (有理数でない数) の集合の濃度はℵ₀よりも濃いことを示し、その濃度をℵ₁とした」
と書いてあった.思わず憤概してしまい, この文を正確に引用するために (買わなくても,出版された本を批判したりおちょくったりする権利はあるとは思うが, 礼儀として ...),apple books で,この本を買ってしまった.
しかも,この著者は,これを,僕も講師を務めたことがある「数理の翼」で学んだらしい. まあ,僕自身も,日本に移住してから,どの数学科からも声をかけてもらうことがなかったくらいなので, こういうことを書く人が出てきても何の不思議もない,と言えるのかも知れないが.
ただし, これは,この著者だけの誤解/無理解/大間違いでもなく,そもそも,世界中の数学者の大半は ordinal number としての $\aleph_1$ を理解していないし (といっても, 数学的には,数学が矛盾しない限り, 誰も永遠に $\aleph_1$ を完全には理解できていないわけだが ... 恐くて,まだ読んでみていないが, この本には不完全性定理を説明した章もある!), 連続体仮説は正しいと,何の根拠もなしに信じているようである. 一般連続体仮説を信じちゃっている節の人もいる.
例えば,
このガモフの 1,2,3...infinity は,politically incorrect であるだけでなく,上の Andres のコメントにある話も含めて,数学的にも色々問題のある本である. ガモフ自身は数学者ではないが,彼はウラムの親しい友人だったので, 数学者から隔離されていたわけでもないはずなのだが ... これについては,また別の機会に書く.twitter をながめていたら, Josephine Baker の生涯を短かく纒めたフランス語のビデオクリップが,目にとまった. twitter では,Alexandre Tharaud を follow しているので,彼の retweet だったかもしれない. 彼女が黒人としてはじめてパンテオン入りすることになった, ということことが契機の post のようだ.
Josephin Baker は,1960年代の,アメリカの segregation に抗議して, 長年住んでいたフランス (彼女は,第二次世界大戦中には,フランスのレジスタンスに参加していたらしい) の国籍をとり, アメリカで舞台に出ることを拒否することになる. でも,Luther King 師の市民権運動には積極的に参加している. しかし彼女の「自分の国」は,本当にフランスになってしまったようである. 彼女が,晩年,「自分の国」となったフランスの社会矛盾には目をつぶって, 「私の国パリ」と歌えていたのかどうかは,ぜひ知りたいところである.
言語の多様性は,楽しい現象だし,言語表現を豊かにするものでもあると思います. しかし,数学や,科学の用語では,不必要な多様性は,さけるべきだと思います.
また,日本語でガラパゴス化と呼ばれる種類の現象は,
十分に国際的でない言語ではつねに起ってしまう危険があります.
僕の Twitter の post でも書いた「幾何級数的」は,ガラパゴス化の典型的な例の一つです,
これについては,前に ここ にも書いたことがありますが,
「マルサスの人口論」(18世紀の本です!) に出てきた用語の訳語が日本語で定着してしまって,
多くの数学の素養のない人が,
これが exponential
という形容詞の離散バージョンだということを理解しないで使っている,
という状況が定着しています.しかも,日本の和英辞書を見ると,
「幾何級数的」 には,geometrical というような使えない訳語しか出ていなくて,
これが exponential の意味だ,ということを,日本人が,理解したり,
それについて非日本語話者と意思疎通することを,ブロックしています.
日本語の 「濃度」では, そのような問題は起っていないとは思いますが,この単語を日本語の教科書で習った学生が, 「濃度」と cardinality の間に関連をつけることができなかったとすると, その効果は「幾何級数的」の破壊的な影響と似たりよったりなものになってしまうと思います.
ちなみに,「幾何級数的」の呪詛のためか,日本人は,exponential growth の概念自身をうまく理解できていないように思えます. このことについては ここ や ここ でも議論しました.まあ,理解ということでは, 日本人の (平均的) 数学者は濃度を理解していない (たとえば,こんな事例),とも言えるので,ここでも状況は 「幾何級数的」と似たようなもの,と言えるかもしれませんが.
ヨーロッパの言語の間では,語彙を十分に共有できるのに,(たとえば,cardinality はドイツ語では Kardinalität フランス語では cardinalité など) 日本語では,それが難しい, というのは,やはり,議論をするための言葉としては,日本語を捨てる方向に向うしかない, と結論づけるしかないようにも思えます.また,ヨーロッパ系の単語が日本語に取り入れられたときに, もとのニュアンスとは異るものに変形されてしまったり, 取り入れた時代の意味を保持しているために, 原語と意味が異なってしまったり (訳語ではありますが, 「幾何級数的」はまさにそのような例と言えるでしょう),というのは,“lost in translation” 現象の要因と見たときには,面白いけれど, コミニケーションに,不必要なバリアを果すものとなってしまうように思えます.
もちろん,日本語を鍛えあげて,英語に対抗できる国際語にする, ということも考えられますが, 誰もその努力をしていないし,逆に,皆が日本語が誤用されるのにまかせている,ように思えます.
以上は,確実に Twitter の字数制限を超えています.
つまり,日本の政治や経済を含めた意思決定は,そもそも, 意思決定をせずに堪えしのぶ,ということが基本行動原理となっているのではないかということである. この基本行動原理を守り抜くためには, リーダーは,何か積極的な行動を起こす意志や能力を持っているべきでない. リーダーにもとめられるのは,民衆の気休めになるような発言を繰り返せることと, 一旦決めたことを頑なに押し通す能力 (または愚鈍さ) だろう. もちろん,意思決定をせずに堪え忍ぶのは,暗く堪え忍んでいる必要はなくて, 酒を飲みかわして楽しくやることもできるし,実際に日本の文化はそのようなものになっている.
そのような文化風土では, もし,積極的な行動を起こす意志を持っているリーダーが出来たとしても, 堪える文化出身の,そのようなリーダーには, 得てして,有意義な行動を起こす能力が伴っていないことが多いため, かえって大変なことをしでかしてしまうことが多く,そのような,ネガティヴな例が, 意思決定をせずに堪える,という戦略を中心に据えた文化を,ますます助長することになってしまう.
もちろんこれはリーダーの側 (だけ) の問題でもないだろう. リーダーが積極的に有意義な行動を起したとしても, それに対する長期的な視野からの評価が,民衆側にできるわけでもなく, 民衆が理解できて,ついてこられる策やそのためのスローガンといえば,結局のところ, 「神風」や,「欲しがりません勝つまでは」や,それらのバリエーションということになってしまうのだろう. しかも,有意な,積極的行動や決断がなされないためのしくみは,社会の組織の各層に張り巡らされている. 例えば,年功序列は,そのための強力な仕組の一つだろうし,専門を細かく分けて, 全体を見渡せる人を作らないようにすることとか,外国語教育をわざとゆがんだ形のものにして, 外国語で考えることのできる人を作らないようにする,というのもその仕組の一部だろう.
だたし,実際には,日本の近代史では,政治や経済や,その他のシーンでは, 画期的な意思決定がなされる例外的な瞬間もいくつかあったわけだが, その画期的な意思決定には, それに続く第2第3の画期的な意思決定が起ることはほとんどなく, 画期的だった事例の続きは,すぐに堪える行動原理による文化で置き換えられて, 次第に意味を失なってしまう,という例が多かったのではいか.
明治初期の近代化はそのような例のひとつだし,太平洋戦争での敗戦に続く軍国主義国家としての日本の 「発展」もそのような例になっていると言えそうである.
日本が,江戸時代を続けて,持続可能性の高い前近代的なシステムを維持していたとしたら, この,意思決定をせずに堪え忍ぶタイプの文化は,愉快ではないかもしれないが, ある種の持続可能性社会として,もっと肯定的な評価ができるものになっていたかもしれない.
19世紀の中ごろに,西欧の意味での近代化に足を踏みだしてしまった日本が, この意思決定をせずに堪え忍ぶ文化を維持して, しかも,その後,ある意味で,ある程度の成功を修めているのは, 上で言ったような,いくつかの「画期的な意思決定がなされる例外的な瞬間」のおかげと,天災や戦争, 外国からの圧力など,この,意思決定をせずに堪えしのぶことによる頑なな持続性を, 外側から打ちくだいてくれる出来事が十分にあったからではないだろうか.しかし,これは, 逆の言い方をすれば,外側から定期的に壊してもらえなければ,成り立たないシステム, ということでもあろう.
[この項はまだ書きかけです.]
I read today a news in the internet that President Bach of IOC (also a German) gave some awards to Prime minister Suga and Tokyo Mayor Koike, apparently for their “special contributions” to Tokyo Olympic Games. Somehow, this reminded me the fake degrees von Sieblold gave in his days to his Japanese students, which was, in a way, also a win-win to the both sides of the parties.
まあ,「坂を転がる」のは,まだ加速運動ではあるが,「爆発的感染拡大」では, 一瞬大きく加速するだけで, あとは慣性運動である. 爆発は,物陰に隠れて,耳をふさいで目を閉じ口をあけて鼓膜が破れないようにして,やりすごせばいいが, exponential increase はそうはいかない.
... と書いてみて気がついたのだが,ひょっとすると,これは exponential と explosive を単に読みまちがえただけなのではないか? 1年ほど前には,小池知事が,「ステイホーム」を 「ホームステイ」と言い間違えたことがあったが,それと同じようなやつなのだったとしたら,大いに笑える.
オリンピックのパラレルワールドでは, 人々が反対はしない (たとえば内乱や内政と解釈して放置してしまう) 戦争で, 兵士でない人たちまでも陵辱され死んでゆく.
小池知事も再三発言しているように,「お家でオリンピック観戦」という形で, オリンピックを,今至急に求められている人々の行動の誘導に利用することはできるだろうし, その際には,オリンピックが,ゲームにすぎないし,戦争ではなくて競争にすぎない, という事実は,とりあえずは,肯定的に評価できるだろう.競争や戦争にならないと何も理解できない, という,人類の習性を助長する,というオリンピックの主要機能の問題点については, この際,とりあえず目をつぶってもいいかもしれない.
オリンピックについては,「観戦」というよりは,「観察」という観点から, 主にネットでチェックしているのだが, 大阪なおみの試合だけは,観戦に近いスタンスで追視 (follow) した.彼女の cross-cultural なバックグラウンドへの共感のために評価があまくなっているかもしれないが,それを除いたとしても, 大半の日本人アスレートが石器時代人なのに対し,近代人である彼女には,empathize できるところが多い.しかし,いずれにしても,彼女が決勝まで進めないだろうことは, 二回戦の後のインタヴューの言明で明確に見えていたので,大敗したこと自身には,それほど驚かなかった.
こう書くと,負けた本人には酷な言い方になってしまうかもしれないが, 決勝よりずっと前に試合をドロップアウトできたことは, 彼女にとっも,我々にとっても,本当によかったと言えると思う.日本が「大阪なおみ」に求めていたのは, 日本に実際には存在しないところの,多様性の,表徴だったので,彼女がオリンピックで優勝して, この役割をフルに果さなくてはいけなくなっていた状況を考えてみると,その場合には, 彼女は,ひどく難しい立場に立たされてしまっていたことになったろうし, 我々は,そのひどく難しい立場に置かれたことで,ひょっとしたら, ひどく歪んだものになってゆくことになったかもしれないところの,彼女の personality のその後の変容を,目撃しつづけなくてはならなくなっていたかもしれないからである.
これは,ベルリンオリンピック(1936) で優勝した, 「実際には存在しなかったナチ政党の寛容性」の表徴の役割を負わされるべく, ドイツからオリンピックに参加したユダヤ人運動選手の運命を起想させるものがある. ベルリンオリンピックでメダルをとった,ドイツチームのユダヤ人運動選手は複数いたが, 「大阪なおみ」は,もし優勝していたとしたら,この,日本の「実際には存在しない多様性」の表徴を, 一人で背負って演じなければならなくなっていたわけである.心の fragility を告白せずにいられなかった近代人としての彼女にとっては, これは,かなりつらい状況になっていたかもしれないような気がする.
[この項はまだ書きかけです.]
日本のメディアも,一番肝心なところを隠す,というのが規則になっているようである. もしこれが規則でない, というのなら,日本のメディアで報道記事を書いている人たちは,頭が狂っている. 実際のところは,日本のメディアで報道記事を書いている人たちは頭が狂っているし, 一番肝心なところは隠すというルールも存在する,というのが本当のところだろう.
今いちばんいらいらするのは,日々のCovid-19の感染状況の報道で, 重症者数や,前は隠していた死者の数は,発表されるのに, その年齢構成が発表されないことである.もし,これが若年層に重心を動かしつつあるのなら, これは老齢者にワクチンを打ったことの効果ともとらえられるが, 若い人は老齢者より重症化してから,長くもつ可能性があるし, 老齢者のように,あるところで見切りをつける,という対応をとられることも少ない可能性があるので, 重症者一人あたりのベットの占有時間がより長くなる可能性があり,その状況が今生じているのだとすると, これから来ることになる感染者のピークから, それと,さらに数週間の時間のずれのあることの見込まれる死亡者数のピークの間に, 医療崩壊と言える状況が生じてしまう可能性が高くなる.
これは,わざと隠しているのか,それとも今言ったような,データの意味が分っていないのか. これも,その両方のような気がする. 頭の狂った人が隠すのが美徳の文化に安住していることの,とりかえしのつかない弊害といったところだろう.
まあ,とりかえしかつかない状況まで進むかどうかは,これからなので, 何とも言えないが,日本にとっては,むしろとりかえしがつかないような状況まで進んで, そのことが契機となって,悪弊が改善された方がいいような気もする.
1964年の東京オリッピックのときに,IOC の要請 (と言えば聞こえがいいが, 要するに強制) で, 当時,冷戦で緊張関係にあった東西のドイツが共同チームとしてオリンピックに参加することになった. 平和の祭典というプロパガンダのための演出といえるだろう.コロナ下での,SS (super-spreader) Olympics で,陽光の下に曝されつつある IOCの欺瞞の体質は,この頃からのものだったことが分かる. 共同といっても, 東ドイツ側のチームのメンバーは,西ドイツの選手たちと交流することは, 同行した東ドイツの幹部にきつく禁止されたということである. 共同ドイツチームは,このときが最後で,これ以来, ドイツの再統合後のバルセロナオリンピックまで,30年以上結成されることはなかった.
ドキュメンタリーでは, この共同ドイツチームのメンバーとして,この東京オリンピックに,当時の東西ドイツから参加して, メダリストとなった人たちや,なりそこなった人たちのインタヴューを中心に, この共同チームの歴史的政治的背景や,共同ドイツチームというアイデアの欺瞞, また,そこから生れた悲喜劇を語るものだった. 当時の選手たち,特に東ドイツからの選手たちが, 未来都市東京について,今でも感嘆の念を持って語っていたのが印象的だったが,考えてみると, タルコフスキーが,ソラリスでの未来都市のシーンを,首都高で撮ったのも, これからわずか7年後くらいの頃だった.
当時のオリンピック選手は, もちろん,今では,もう,そこそこ高齢で,映像に付け加えられた字幕によると, インタヴューの後で亡くなった人もいた.
僕はその当時,東京の郊外の小学校の4年生で,もちろん,当時の東西ドイツの政治的な背景について, 知りようもなかったし, 回りの大人たちだって,誰も世界で何が起っているか分っていなくて, 日本人が沢山メダルをとったのを単純によろこんだ,という程のレベルの現実認識だったのだろう.
しかし,考えてみると,僕の子供時代は,まさに,このオリンピックによって形成された,とも言える. 僕の子供のときに住んでいた東京の郊外の場所には, このオリンピックにむけての東京の都市整備のための立ち退きで強制移住させられた人たちの住む, 「都営住宅」という名前のスラムがあり, そこの子供たちと折が合わなかったことが,僕の小学校時代の concerns の大きな部分を占めていたからである.
この東京オリンピックでは,小学生の僕は, 新聞のオリンピックの記事の切りぬきを集めてアルバムにしたので (これが小学校で出た課題だったのか, それとも自主的にやったものだったのかは,もう憶えていない), ドイツの共同チームのことも,その時の新聞記事に書いてあったこととして, うっすらと憶えている. 今調べてみると,日本語では, 「東西統一ドイツ選手団」と言っていたようである.当時のドイツ語では „die gemeinsame Deutsche Mannschaft“ とかなんとかだから,この日本語表現よりは、 ずっとそっけない (nüchtern な) ものになっている. 開会式のときにブルーインパルス (当時は F-86で飛んでいたと思う) が, 都心の空に描いた五輪の輪の端が,小学校の校庭から,東の空に見えた.
ヨーロッパ語の表現も,日本語の表現も, 両方とも,未来への責任の放棄に対しての批判として用いられることが多いが, 「行動の人」たちは,「いちかばちかやってしまえ」という, 前向きの表明として用いることもあるようである.そしてこの2つの意味の重みの分配が, ヨーロッパ語の表現と,日本語の表現とではかなり違うかもしれないのである.
ヨーロッパ語での表現の方は, ドイツ語のものが,この «le déluge» が,ドイツ語版で旧約聖書のノアの洪水のことを指していることが, 一番はっきりとわかる („Sindflut“ は人間の sin (Sünde) を罰するために神がつかわした洪水 (Flut) という言葉の由来が,現代ドイツ語の話者にも分かる単語である). 英語版では, “the Deluge” と大文字で書いたので,こう書けば,聖書を知っている人には, 普通にはノアの洪水のことだと分かると思うが,小文字で書かれることも多いようである.
僕は,ドイツ語経由で,この表現を学んだので,この表現での聖書のノアの洪水のアリュージョンは, 当然,皆分って使っている思っていたのだが,ネットで検索すると, 英語の解説文で,le deluge は聖書のノアの大洪水のことだと,わざわざ説明しているものがあるので, 背景を知らずに,ただの洪水のことと思って使っている人も少なくないのかもしれない.
ドイツ語版の „Nach mir die Sindflut“ は,マルクスの,Das Kapial にある,
In jeder Aktienschwindelei weiß jeder, dass das Unwetter einmal einschlagen muß, aber jeder hofft, dass es das Haupt seines Nächsten trifft, nachdem er selbst den Goldregen aufgefangen und in Sicherheit gebracht hat. Après moi le déluge! ist der Wahlruf jedes Kapitalisten und jeder Kapitalistennation. Das Kapital ist daher rücksichtslos gegen Gesundheit und Lebensdauer des Arbeiters, wo es nicht durch die Gesellschaft zur Rücksicht gezwungen wird.との関連で連想されることが多いようだ.この連想の方は,実は,僕は最近まで気がつかないでいた. しかし,たしかに, „Nach mir die Sindflut“ は,トランプ前大統領の „Wahlruf“ (スローガン) だと考えてみると, ジャストフィット感がある.
一方, 「後は野となれ山となれ」は,近松の『冥土の飛脚』で,都落ちした(この場合の都は大阪) 忠兵衛の 「栄耀栄華も人の金、 はては砂場を打ち過ぎて、あとは野となれ大和路や」という台詞からきているらしい. ちなみに, 「砂場」は,そこが大阪城築城の際に砂の deposit として使われたことからきた地名のようである. この由来から, 日本語の,こちらの方の表現は, 上で言った, 「いちかばちかやってしまえ」の方の意味が勝っていて, 「未来への責任の放棄に対しての批判」の方の意味は, ヨーロッパ語での表現を知っている人だけに共有されているものなのではないか.
しかし,まさにこの,ヨーロッパ語の表現と,対置される日本語の表現の意味の違いから, たとえば,温暖化の議論で,英語での «Après moi le déluge» (英語でもドイツ語でも, ちょうどマルクスのテキストでそうだったように, 教養を誇示したい人が, フランス語やラテン語のフレーズをそのまま引用することが少なくない) と言ったのを 「野となれ山となれ」と訳したとき,翻訳で失われてしまう意味 (lost in translation!) は小さくないのではないかと思うのである.
[この項はまだ書きかけです.]
政治的 [理想としての言葉の解釈]: 目先の利益しか考えられない人(集団/団体) のことも配慮する.
政治的 [現実的な言葉の解釈]: 自分の目先の利益しか考えられない.
あるいは,
政治的 [理想としての言葉の解釈]: 現実をパワーゲームとしてしか見られない人 (集団/団体) もあることを想定して, それらの反応も予測して,規則や法令等を設定する.
政治的 [現実的な言葉の解釈]: 現実をパワーゲームとしてしか見られない.
この文章は,“Surely You're Joking, Mr. Feynman” にも収録されていて,この本は, 大昔,まだ学生だったころに, 英語でのコミュニケーション力を上げるのには,簡単なことが簡単な英語で書いてある本も読むべきだ, と思って読んでみたことがあった.いまこの文章を読み返してみると, politically incorrect な,つっこみどころ満載の,この文章では,ファインマンの言っている Cargo cult science を催行している人たちは,単に救いようもなく naïve なだけ,というような立場で書かれているが,これは,もともとの cargo cult も含めて,単純化のしすぎなのではないかと思う.卒業式講演の趣旨としては, 「注意しないと気がつかないうちに cargo cult science をやってしまっているかもしれないので,そうならないように気をつけましょう」というような, 寺田寅彦の書いたものを読んでいてもよく出てきそうな,お説教になっているが,現実の,cargo cult の成立には,自分の立場や,利益や,判断や,決定の権威付け, (個人レベルでは,自己肯定のためのこじつけ等) というというような, モティヴェーションの占める割合が,実は非常に大きいのではないだろうか.
パプアニューギニアの先住民の執り行ったというカーゴカルトや, ほとんど同じ種類のことかもしれないが,(ローマや天竺などの先進文化から取り入れた, あるいはそれらを模倣して創作 (これはまさにカーゴカルトである) した) 宗教儀式の執行や, (また,これも同じことの特別な場合にすぎないかもしれないが) オリンピックゲームの誘致/代行, など,カーゴカルトに分類できそうなイベントの背後にある, と思われる力学を考えてみると,単なる naïvety だけではないものが強く感じられる. もともとのカーゴカルトだって,これを執行する司祭たちにとって,飛行機のダミーを作って儀式を行なうと, プレゼントを持って本物の飛行機が降りてきてくれること (を自分たちが信じていること) かどうかが問題なのではなくて, 問題となっているのは,むしろ, これを半ば信じて民衆が自分達を司祭としてまつりあげてくれること, あるいはまつりあげてくれることになっていること,の方なのではないか.
神道の結婚式は,明治維新以降にキリスト教の結婚式を真似て体系化されたということだが, ここでも,キリスト教の愛 (性愛ではない, あるいはそれを単に部分として含むもっと大きなプラトニックな) は,飛行機のエンジンと一緒に置きざりにされている(*).
Cargo cult science に至っては,「応用」と称して,科学を悪用して得をすることが奨励されている文化では, その影に隠れているものは, 単に,この cult の儀式を執り行う人たちの知性のハンディーキャップだけでなく,もっとずっと多様なものがある,と考えてよさそうである.
ここで,その多様性について,総括的な分析をするのは無理かもしれないが, その一つである,「科学」を権威として悪用する, という基本パターンについては,ひとこと言っておいてもいいような気がする.
念のために言っておくと,今,上で「悪用」と書いたが,どんな cargo cult science でも,その運用によっては,その結果が否定的なものになることも, 肯定的になることもありうる. ここで問題としているのは,cargo cult science であるかどうかで,特定の cargo cult science の (たとえば社会的な) outcome の是非ではない. このことも含めて,次の例は,ここで言っている意味での cargo cult science の典型的なものの一つである:
スーパーコンピューター 「富岳」で新型コロナウイルス対策を研究する理化学研究所のチームは4日、会話の際などに口から出る飛沫 (ひまつ)の飛散シミュレーションや実験に基づき、 不織布マスクは鼻に当たる部分のワイヤを曲げて顔との隙間(すきま)ができないように着ければ、 二重マスクと同等の飛散防止効果が見込めるとの解析結果を発表した。ネット上の報道でのテキストの一部だが, ここでは,この報道をしたメディアの批判が主題ではないので, あえて意図的にテキストのソースは明記しない.
ちなみに 『「富岳」による新型コロナウイルス対策の研究』の報道自体は,日本人の大半が, マスクをすることに納得することになった鍵の一つだったと思われるので,この種類の報道の日本での社会貢献ははかり知れない. しかも,この報道は,海外のメディアでも取り上げられたので, 社会貢献は日本に限定されるものですらなかったかもしれない. 石器時代人が大半を占める日本人 (および,世界の人類) を納得させるためには, 「富岳」という古代宗教の神は,いずれにしても必要でもあったのだろう.
しかし,この種類の報道 (公立の研究機関で発表されたテキストも似たようなものだったが, この場合,公立の研究機関は,予算をとるために,ぜひとも石器時代人にアピールする必要があるのだろう) は, 「科学」を権威として悪用する (まあ,ここでの場合では,更に,悪用されているのは,科学でもなくて,単に 「富岳」というスーパーコンピュータにすぎない,とも言えるわけだが),という意味でのカーゴカルト以外の なにものでもないように思える. この報道では,「富岳」でやったので権威があって正しい,という邪悪な含みが強く感じられるだけでなく,もし, これが「富岳」でなく, ワークステーションで同じことができたときには, その方が (パワーが劣る計算機に乗せるためにはより高度な計算のテクニックが必要になるという意味で) すごい, という (科学的ではないにしても技術的な) 価値観すら欠落しているし, 力まかせに,かっこいい名前のついたスーパーコンピュータで計算してみただけ,ということに対する羞恥も感じられない. もしそうでないなら --- たとえば,理論的な計算量の下限から,これが 「富岳」でなくては実現不可能,ないしは,現実的な時間内に実現不可能ということなら, その議論自体は正当な計算機科学になりうるだろうが,そのような趣旨の報道やレポートはどこにもなかったような気がする.
[この項目はまだ書きかけです.]
(*) おまえに,そんなことを言う資格があるのか, というつっこみがあるかもしれないので,あらかじめそれに答えておくと, 僕の学問的祖先 (博士論文の指導者を親と見てたどったときの家系図に含まれている人々 --- https://fuchino.ddo.jp/Math-genealogy-fuchino.html を参照) には, 新プラトン学派の創始者 Marsilio Ficino も含まれている (名前が似ているだけではなく本当の祖先である --- Ficino とその思想については,山田五郎の 「オトナの教養講座」のボッティチェルリの 『春』 の回に,popular な解説がある).
... しかし,この表明自体,実は祖先の権威をかさにきた, カーゴカルトサイエンスそのものかもしれない.僕の博士論文の価値は読んでみればわかるので, その指導者の指導者 ... をたどった過去に Marsilio Ficino がひかえていることは,僕の博士論文の価値とは全く関係がないからである.昔,僕の祖母が, 健康や医学についておかしなことを言ったことを指摘されたときに「私だって医者の娘です」 (祖母の家は,江戸時代,多度津藩の御典医だった) といきまいていたが,冗談でちょっと言ってはみたが, それと同類の後味の悪さの残る発言だったかもしれない.
もちろん,現在の北朝鮮や中国で, 「自主的な研究結果」が,どのような懲罰を受けるだろうかを思い浮かべてみれば, 現在の日本は,それよりはずっとまし,と言うこともできるかもしれないが ...
日本を含めた,これらの北東アジアの国々の傾向を他の文化圏の国々と比較してみると,文化社会学的な疑問が色々と湧いてくる. たとえば,これは, 東アジアの土着人の愚鈍性の現れということなのだろうか (僕自身は, 「愚鈍性の保存則」というタイトルでも表現しているように,国, 文化圏など,ある程度の大きさを持つ単位で全体として見たときには, 愚鈍の総和はどこもそう変るものではなくて,ただその性質や分布の仕方が異るだけなのだ, という思い込みがあるのだが ...).あるいは, 東アジア的な農耕社会というような, 文化の共通の背景がファクターになっているのか.等々. もっとも,農耕社会的非民主主義というような社会構造は,東アジアに限ったものではないのかもしれないが.
これに加えて,自然災害に恵まれた(?) 日本の場合, この,北朝鮮や中国よりはマイルドかもしれないとしても,どうしようもなく非知性的な, (知性的な) 意思決定 (の不在) の背景には, (バッハ会長も言うような) Japanese resilience と言えば聞こえがいいが,要するに, 外から完全に壊してもらえるまで,自分ではシステムを入れ替えたり,本質的な改良を 図ったりすることができない,という特性が, 加わっている,ということではないのか.
[21.07.23(金10:19(JST)) の補足] 現在, まさに,行なわれようとしているオリンピック/パラリンピックは,この, 「外から完全に壊してもらう」, ということの契機になるかもしれない.前の大震災では, 完全に壊してもらいそこなっていたので,これは,希望の光りと言えるかもしれない.
Covid-19 の方は,まるで生きてでもいるように,variants を次々と送りだして, 人類への世界的規模での感染,という,胸がすくような成功の道を,突き進んでいるように思える. 失望どころか,賞賛の念すら湧いてくる.
これからワクチンの接種率が上がってきたときに,人間の側の,軽率な/馬鹿な行動との兼ね合いで, Covid-19がどのようなあざやかな行動に出ることになるのかは,楽しみだ,と言うべきか, 考えるだけで恐しい,と言うべきか.
アメリカ経済学の基本的な考え方の一つに,人間や,人間の社会や国家は, insentives の設定如何でどのようにでも行動してしまう, というものがある.というより,そもそも,ここでは,insentives が行動を規定していて,モラルや理想主義や自由意志は, この経済理論には存在しない. もちろん,この経済学を確立した経済学者たちも,そのような行動原理の束縛から自由であるわけではなく, 社会主義を悪く言うと褒められる, という,アメリカの (かつての? --- ちょっと前にまだ前大統領が大統領だったときの,彼の “communists” という罵倒の言葉を思い出してみると, これは過去のことではないようにも思えるが...) 時代の insentives に踊らされて, この insentives に関する理論をベースに, 公共事業が,自由経済に比べて如何に効率が悪く,間違った結果を招くか,とう議論を延々と繰り広げたりする.
Insentives が insentives として機能するにあったっては,人間の側の動物的な欲求が, そのベースになっているわけなので,この動物的な欲求が正に動物的であることにより, その insentives に対応する反応は,常に present biases につきうごかされた, しかも,きわめて非論理的で動物的な (つまり,きわめて “人間的な”) ものになる. この “きわめて非論理的な” が,実は,しごく予測可能な,単細胞的なものである, というのが,現代の行動経済学の説くところで,この理論を, 自分が得をするための「実学」と理解する人は,理論の説く,あさはかな insentives につき動かされた行動の裏をかいて利益を得ようとする,という,これまた,あさはかな行動に出ることになる.
Covid-19に関する,世界のニュースを見ていると,この,人間は,insentives につき動かされて,単細胞的に (あるいは単細胞の集積としての集団として) 行動する, という世界観の正しさを納得させられることが多い. しかし,この見方をしたときに,ほとんど自明に導かれる幾つかの帰結が,見過されているようにも思える.
その一つは, 今,Covid-19のためのワクチンを開発製作/販売している製薬会社に関するものである. 製薬会社が世界を制覇つつあるということは,たとえば,弱小国であるとはいえ, 一国の総理大臣を呼びつけたりすることができたりするのを見ていると, 納得できるだろう.しかし,製薬会社にとって何が得かと考えてみると,Covid-19 が variants を蓄積して, ワクチンをすりぬけてしまうようになること,は,当然,彼等にとっての究極の利益となる. そうなったときには,新しい,危険な variant に対応するワクチンを,再び世界規模で接種する必要が出てくるからである.
今, 人々の 「コロナ疲れ」のために, 色々な既成のたがをはずしたがっている国や,オリンピックを是が非でも実行しようとしている国や, CDC のように,ワクチンを接種した人は何をしてもいい, と言っているに等しいようなガイドラインを発表してしまう健康衛生組織などが世界中でたくさん出てきているが, これらの「対策」の裏にワクチンを製作している製薬会社たちの圧力や manipulations が何もかかっていない, という可能性はあるのだろうか? かつて米国の煙草産業が,煙草の害に関する医学研究を買収しようとしたようなことが, ここで起っていないとしたら,それは,むしろ奇蹟であるように思える.
この映画のもっと不思議なところは,Berlinale で受賞した映画なのに, ドイツ語でサーチすると,どこにも受賞のニュースが出てこないことである. 一方,英語でも,フランス語でも,普通に検索にかかるし,The Guardian には,大変に positive な批評が載っている.
ドイツ文化は (そして,これは日本文化や他の文化でも同じだが), 何でも正しく評価できるわけではなくて, それが全く理解のできないものものも多くある (たとえば Fauré の音楽は, ドイツ文化の理解のできないもののうちの典型的なものの一つだろう) 「偶然と想像」も,何かのドイツ文化のタブーに触れたのか, あるいは,Fauré の音楽のように,ドイツ文化の死角に入ってしまったのか, あるいは,ドイツ人は,思ったよりもクラシック音楽に理解があって, 僕と同じように,リズムの間違いに我慢ができなかったのか ... タイトルだけに関しては,„Zufall und Imagination“ として, 英語でよりずっと直球の翻訳ができるはずなのだが ...
ちょっと気になって youtube にある,子供の情景の第一曲目の演奏を色々聞きくらべてみたが, 聴いた限りでは, 出だしの部分を三連符のイアンビックににくずして演奏しているヨーロッパやアメリカのピアニストは一人もいなくて, 逆に,ホロヴィッツのように,符点音符に符点を2つつけて,32分音符で弾いているものもいくつかあった. 日本人の符点音符が一般にあまいのと, 日本人が子音に母音を付加しないと発音できないことの間には,相関関係があるかもしれない. 逆にホロヴィッツの32分音符は,独立していて二重三重にもなったりする子音が重要な役割をはたす, ポーランド語の発音と関連しているのかもしれない. もしこの相関関係が間違っていないのだとすると,濱口監督の映画の背景で鳴っているのは, 日本語なまりの子供の情景,ということになるのかもしれない.これを検証するには, やはり子音に母音をつけないと単語を閉めくくれないイタリア語の話者の演奏を聞いてみることかもしれない.
この文章は,Google translate にかけて読んでみる人がいるかもしれないので, そうやって読んでも, (出力が英語の場合に) 書いてあることが,ある程度,想像できるようなものが出力されるように, 文章を調節してみたが,それでも,自動翻訳してみると, ところどころ驚くべき結果が出てくる. Google translate は文語 (特に漢文調の文語) が全く翻訳できないようである. ちなみに,この文の翻訳では,「文章」,「文語」,「漢文調」の訳語は, 全く misleading なものになっている. 主語の補完も,多少 semantics に踏み込まないと主語が確定できないような場合では,全滅である. ここでは,“lost in translation” はジョークでなく現実である.
昨今の,巷での, 「自由」や 「独立」の使われかたは, 「本能に従って生きられること」という言い換えで説明できるものであることが,多いようである. このことは,covid-19 と関連する表明でも,明確に観察できる. もっとも,人類の行動をつきつめて観察してみると, 「本能に従った」ものでないものを探すのは,難しいかもしれない. 「理性」だって,つきつめれば「本能」ではないのか?
そうであるかもしれないが,僕がここで言いたいのは, とりあえず,人間の (集団としての,あるいは個体ごとの) 活動の動因となっていると思われる行動原理を,本能,文化/伝統, 理性,と3つに類別してみることにしたとき,そのようなラフな類別の意味での 「本能」に属す行動を,擁護するための言い訳として,「自由」や「独立」という単語が巷で用いられることが, 多いのではないか,ということである.
このような類別で,何が,「本能」に分類できるのか,というのも依然として難しい問題だが, ある行動様式が, 人類の,どの時代の,どの文化でも観察できて, その行動の祖型と言えるものが,人間以外の動物でも観察できるときには, それを本能に分類してもいいのではないだろうか.
たとえば,人間の宝石貴金属に対する嗜好は,そのようなもの,として理解できるだろう. 宝石貴金属に対する嗜好や,それに基く,価値観や,権威や権力の誇示の体系は, ほとんど,どの時代の,どの文化でも観察できるし,既に前にどこかでも書いたように, 胃石になるものを探しだして飲みこむ,という動物の行動 (本能) は,その嗜好の祖型になっているように思える.
抱擁や愛撫に対する欲求も, 「本能」に属すことを, 同様に結論づけることのできる人間の行動だろう.胃石を飲みこむという行動様式は魚類にもあるのに対して, 抱擁や愛撫の行動本能は,生物の発展段階では,恒温動物以降に本能に組み込まれた行動原理であるように思える. 人間が,恒温動物には感情移入しやすいが,魚や両生類などには感情移入しにくい, というのは,形態の異差もあるかもしれないが, 抱擁や愛撫の行動様式の有無が,決定的な要因なのではないか?
この抱擁や愛撫の意味は,体温保持の戦略,ということを別とすると,バクテリアやヴィールスの共有による herd immunity の確立を目的とした生存戦略だろう.この戦略が人間以外の動物にとっても, いつでも,優れたものであるわけではないことは, 感染病で,絶滅寸前の種が滅んでしまう,ということが時々起ることからも明らかだが, 人間の場合には,社会形態の進化や,医療の進歩から,他の動物に比べて, この herd immunity の戦略が意味を持ちにくくなっている,ということが言えるのではないだろうか.
医療が進歩していない未開社会なら,感染症が発生したときに,発症した個体を全部処分してしまう, という対処と,本能に身をまかせて herd immunity の確立を促す,という対処を平行して行なう, という戦略で,死者を沢山出しても,群としては感染症をサバイブする, ことも,可能かもしれない. ブラジルのように, ほとんどそれに近い戦略をとっている国もなくはないが (しかもブラジルの場合にはその戦略が民衆に支持されている !), 現在の文明は,そのようなアクションが意味を持つようにはデザインされていないように思える. しかし,人間の本能の方は, 旧式の抱擁や愛撫による herd immunity の確立の戦略を, どうにも変えがたく保存しているようである (ブラジルで革命が起こらなかったり, 今だにトランプ元大統領の支持者が根強く残っていることも, その証拠の一部と解釈するこができるだろう). 「自由」という言い訳は,そのような本能の擁護のため,„Querdenker“ たちによって 表明されることが多い.
全般的な意味での依存症が,生存本能の副産物のようなもので,だから,やはり本能に分類できるものだとすると, 合法ドラッグスを擁護するためにもよく使われる「自由」という言い訳も, ここで言っているような本能の擁護としての「自由」の項目に加えることができるだろう.
ちなみに,これはちょっと議論がわき道にそれてしまうが,herd immunity の確立を促す戦略と, 種の進化 (というか変化) の速さには関係があるのか, というのは,非常に興味深い設問であるように思える.ヴィールスが動物の DNA の変異にどう貢献するのか, ということに対する分子生物学での答が,この問いに対する答の鍵になるわけだが, 先程,言った, 抱擁や愛撫の行動様式が主に恒温動物以降に本能に組み込まれた行動原理であることを認めることにして, 恒温動物以降の進化の枝に乗っている動物の変異の速さが, それ以前のタイプの脊椎動物に比べてずっと早いように思えることは, ビールスが DNA の変異に有意に貢献している, という仮説を示唆しているように思える.
一方, 科学者にとっての「自由」は, 上で言った本能の擁護としての「自由」とは,真逆の意味を持つことが多い.
初期の現象学でも議論されているように,我々の認識は,本能や,既成文化の押し付ける価値観や, 我々自身の思い込みなどによって曇らされていて,そのために,本来,認識できるはずのことが,認識できないでいることが多い. 科学者にとっての自由とは, そのような,本能や既成文化の押し付ける価値観や,我々の思い込みなどからの,自由である. 政治や経済などの institutions が強制する結論からの「独立」も,この自由を確保するための大前提となるだろう. 幸に,純粋な純粋科学であるところの数学では,政治や経済からの圧力は,少なくとも, 直接的な形で受けることは,あまりないかもしれないが, 研究費がとりやすい研究テーマ, 論文が量産できそうな研究テーマ,一般受けしそうな (想定される) 研究結果,発言など, 純粋な科学の自由から足を踏みはずしてしまいかねない,insentives の誘惑には事欠かない. 実際, 近年の日本では,これも,多くの場合,数学以外であるが,滑稽なまでに足を踏みはずしてしまった例が, (メディアで報道される種類の例としても,メディアに登場する自称「専門家」の人たち, としても,または,メディア自身の報道の仕方でも) 頻繁に観察できる.
カントルが「数学の本質は,まさにその自由性にある」と言ったとき(1), この「自由性」は, 当然,上での, 「本能の擁護」とは真逆の意味のものであるが,そのような意味の自由性を理解できない人が多数いる, ということも,また,銘記する必要があるかもしれない.
[この項目はまだ書きかけです.]
(1) このカントルの言葉は,コンテキストから切り離されて引用されることが多いように思われる. この前後の文脈を含めたカントルの発言の,私の日本語訳は,数年前に発表した
カントルの精神の継承 — 無限集合の数学/超数学理論としてのカントルの集合論のその後の発展と,
その「数学」へのインパクト,
数学文化, No.29, 26--41, (2018)
にある.
これではまるでゲーデルの不完全性定理ではないか!
ゲーデルは,アメリカの市民権を得るときに,アメリカの憲法を精読して,この憲法には loopehole があって,合法的に独裁国家に移行できる可能性があることを発見した, というのは良く知られている逸話である. 市民権を得るためのインタヴューに保証人のアインシュタインとモルゲンシュタインに付きそわれて出頭したときに, ゲーデルが,このアイデアについて,試問官に細説しそうになって, アインシュタインとモルゲンシュタインがあわてて制止した,という話は,Dawson の “Logical Dilemmas” にも書いてある (*).
ゲーデルのこのときの考察がどんなものだったのかは,分っていないが,もし, その「合法的に独裁国家に移行できる可能性」のためのステップの一つに大統領が自分自身に恩赦を出す, というのが含まれていたのだったとしたら,笑ってしまうしかない.ただし,この場合, 笑われるのは Fox News におどらされて,今でもトランプ大統領の言うことを何でも鵜呑みにしてしまっている, ほとんど全人口の半数に近いアメリカ国民や, 票を集めるためならトランプでも誰でも擁立してサポートしてしまう某政党だろう.
(*) これは作り話である可能性もある.Morgenstein の日記の1947年12月07日の記載には, この二日前のゲーデルの最高裁でのインタヴューのことが書いてあるが, 上で書いたインタヴューでの逸話には触れらていなくて,書いてあるのは, アインシュタインの最高裁への道すがらに言ったジョークのこととか, そのとき交された数理経済学についての議論 (「天体系の安定性についても何も分っていないのに, 経済系の安定性なんて議論ができるわけがない」とゲーデルが言ったとある)また, この議論から横道にそれて天文学の話など, のみである.ゲーデルがアメリカの憲法に独裁制に移行する矛盾を発見した, ということ自体は事実のようである.今ちょっと見つけられないのだが,これは Morgenstein の日記のどこかにも書いてあったと思う. Morgenstein の日記は,何かを探すために 読みだすと,面白いのでつい探していることと関係のない事項まで読みはじめてしまうので,危険である.
これは取り下げたということではなく, 一時的な措置ということのようであるが,そうだとしても,嘘は,SARS-CoV-2 に感染していない大統領が言っても, SARS-CoV-2 に感染している大統領が言っても, 嘘なのではないか? Biden campain のこの措置 (これは Biden 旧副大統領自身の指示ということである) は,アメリカ文化の真実に対する真摯な姿勢の欠如を露呈しているように思える.
もしろん,「真実に対する真摯な姿勢の欠如」ということで言えば, 日本やその他の,アメリカ以下の国は山のようにあるので,これはアメリカ文化の批判ではなく, 単に事実確認にすぎないのだが.
しかし,それでは,アメリカ大陸で多くの黒人が命を失なっていることは, どう説明できるのか? アフリカ大陸とは違う種類の人口密集を持っている都市の存在や, 黒人の人たちの置かれている社会的状況や,政府の間違ったコロナ対策などが, その説明になるだろうが,もう少し考えてみると,少なくとも米国では,黒人の人たちのうち, 祖先の誰かが白人のレイプの結果生れている人が少なくないようなので (たとえば, この記事 を参照), 実は,COVID-19の重症化危険因子になっているネアンデルタール人の DNA を持っている人が少なくない, ということも背景にあるのではないだろうか,ということに思いあたる.もし,そうだとすると,現代のアメリカの黒人の人たちは, 現在の差別だけではなく,過去の差別の残滓にも苦しめられていることになり, これでは踏んだり蹴ったりではないか.
しかし,僕は, この逸話の解釈を全く間違ってしていたようである. 損得や都合とは独立な真理に奉仕するのが honesty である,というアイデアは確かに日本文化には欠けているかもしれないが (日本語には honesty の適訳となる単語すら存在しない!), このワシントンの逸話 (現在では,実は,これは伝記作家の創作であったことが分っているのだが) が, 逸話として成立するという, まさにそのことが,アメリカが,この意味での honesty に欠けている人に満ちみちている, ということの証明になっているということにすぐに気づくべきだった.もし,アメリカが honest な人たちの国だったとしたら,ワシントンの桜の木の逸話は,あたりまえの話で, 説話としてわざわざ述べる必要がないからである. この話が,アメリカで有名な話である,という事実は,アメリカが,honest な人の 国でないことを憂いている人が少なくない,ということの説明にはなるかもしれないが.
子供のときに,このことに気づけなかった,というのは子供の僕の素直さを記録するものだったのか, 将来の,つまり今の僕の知性の限界を暗示するものだったのか.
今の僕の方は,アメリカの “fake news” やドイツの „Lügenpresse“ にどっぷりとつかっているので, トランプ大統領に対するネガティヴな評価に耳をかたむけがちなのだが,しかし, 「トランプが悪い」というのは, いずれにしても全く的はずれな評価だろう.「悪い」としたら,それは,彼を過半数のアメリカ人が選び,今でも, 過半数近くのアメリカ人が彼をサポートしている,という,そのことだろう.もちろん “America First” は,「自分 (の国) が得をすれば嘘をついても何をしてもよい」ということなので, この 「America」を,他のたとえば「日本」に置き換えれて考えてみれば分かるように,そのように思っている人が過半数である, ということ自体は,何の不思議でもない,と言えなくもないとも思えるのだが … .
日本がアメリカに占領されていた時代からいくらも時を経たずに生れた人間として, かつて日本を占領していたこの国が,meritocratic な理想の国であってほしい, という願望を,僕は,今でも心のどこかに持っているのかもしれない.
大阪なおみさんの試合のボイコットを応援します.記事に対するコメントには, 警官を無視して車の中に入ろうとしたので撃たれても当然,というような意見を言っている人もいましたが, アメリカの巷の黒人の人たちは白人にいつ銃殺されるかもしれない, というリアルな恐怖を常に持って生活しています. 犬が本当に恐い人が,犬から逃げると犬の狩猟本能のスイッチを入れてしまってかえって危険な目にあう, と十分に分っていても,恐くてつい逃げてしまうのと同じようなことが起っているのだと思います. だから,撃たれても当然は, 今 BLM 運動が問題にしている, このアメリカの (そして多分アメリカにかかわらず, そして,この問題を含むもっと一般的な問題に対する) 社会背景を無視した暴言だし, もし仮に (これは英語なら仮定法で書いているはずの文章です) 撃たれても当然というのが正しい批判だったとしたとしても, アメリカでも議論されているように, ではなんで7発も撃ったのか (8発という報道もあったようですが) というのは,当然のこと問題になるはずです.
あらためて,もとの詩と高橋悠治のスコアに引用されている日本語訳を読み比べてみると, この日本語訳はちょっと問題に思える. ドイツ語の詩では,言っていることのロジックが重要な役割をはたしているものが少なくないのだが, これを日本語の雰囲気をあらわす表現に訳してしまうと,もとの詩にあったものがなくなってしまう. ドイツには Goethe の „Über allen Gipfeln ...“ のロシア語の訳をドイツ語に訳し戻したらこんな変なものになった, という (古典的な?) ジョークがあるが,これを日本語の翻訳でやったら, ジョークはもっと可笑しいものになるだろう.
多分,Brecht は,彼の詩を Heine の「死, それはひんやりとした夜だ」を頭に置いて書いているのだと思う. Heine の詩では,Nachtigall が死の世界の夢の中で恋の歌をうたうのに,Brecht の詩では, Amsel が,彼がいなくなった後の世界で朗らかに歌うことが想像される.
「慈善病院」については,「慈恵病院」が固有名詞なので「慈善病院」も固有名詞でおかしくないのだろうが, これがシャリテとは全く結びつかなかったので,それを知って非常にびっくりしてしまったのだ.
折しも (このパグラフは 20.09.08 に書いている),数日前にロシアの野党の政治リーダーの Alexei Navalny がシャリテに緊急入院して, 医師団が毒殺未遂の可能性が高い,という見解を発表した,というニュースを読んだところだ. このシャリテのニュースは, この事件をはじめとして, 旧白ロシアのデモや,アメリカで起りつつあることなど,今,世界の歴史が, どちらに向うかで非常に異なった未来が待っているような, そして,そのどちらに向うかの選択が,胡蝶効果のような偶然に任されているように思える,大きな岐路に立っていることを, 暗示しているように思える.
アメリカ経済学の勉強では (「アメリカ経済学」と言っているのは,主に 北米人の著者たちによる米語で書かれた教科書で勉強したからであるが) この Economics 2.0 の可能性を考えるための基礎知識の習得,ということもその目標の一つだった.
でも,ここで書いてみたいと思ったのは,これとはちょっと別なことである: この「アメリカ経済学」の勉強の後, 日本ではこの「アメリカ経済学」がどう捉えられているのか,という興味からネットを検索してみたら, 日本の大学の経済学の先生と思われる人のスライドで, 次のような驚くべき日本語への訳文をみつけてしまったのだ.
『経済学』
Economics: An Introductory Analysis, 1948
「経済学とは、人々ないし社会が、家計の媒介に
よる場合よらない場合いずれも含めて、いくつか
の代替的用途を持つ稀少性のある生産資源を用
い、時間をかけて様々な商品を生産し、それらを
現在および将来の消費のために社会の色々な
人々や集団の間に配分する上で、どのような選
択的行動をするか、ということについての研究で
ある。」
このスライドのページを書いた人の批判をすることがこの作文の趣旨ではないので, 出典の明記はあえて控える.ここで言いたいのは,これが意味をなす日本語の文章とは思えない, ということである.
「アメリカ経済学」の学習の成果で,原文がどんなものだったか,という想像はつくので, その想像をたどってネット検索した結果,この引用文の原文は Samuelson の Economics: An Introductory Analysis (1948) ではなく,同じ Samuelson が共著者になっている Samuelson, and Temin: Economics, 10th edn. New York: McGraw-Hill (1976), p.3 にある次のような文章 (のうちの最初の文) であるらしいことが判明した:
Economics is the study of how people and society end up choosing, with or without the use of money, to employ scarce productive resources that could have alternative uses, to produce various commodities and distribute them for consumption, now or in the future, among various persons and groups in society. It analyzes the costs and benefits of improving patterns of resource allocation.
こちらの方は訳文とは違って,すんなりと意味が通る. 経済学での特有の概念をあらわす, “scarcity”, “productivity”, “resources”, “alternative”, “costs”, “benefits”, “resource allocation” などという単語がちりばめられてはいるが, これらの単語は, 日常語の意味でとっても文章が意味をなすような使われ方で,文章の中に組み込まれている.
日本語の文章がこの Samuelson and Temin の文章の翻訳なのだとしたら,“people and society” のところで, 既に,誤訳がなされている.ないしは,訳した人は原文の背後にある経済学的な意味を理解しないで翻訳している. 経済学では,個人, 企業,国家経済, 国家政治など異るスケールや目的の組織の行動がすべて同じ経済原理で説明できることを仮定して議論を展開するので, このことを頭におくと,「人」と「社会」を「ないし」というふたつの alternatives 並列するための connective でつないたものとして訳してしまっては,いずれにしても misleading である.money は,ここでは貨幣経済の「貨幣」なのでこれを家計と訳すのは 「ちはやふる」的でしかない.now or in the future は,現在 consume されたものは未来には consume できないので (opportunity costs!), 「現在および将来」 では論理的にも破綻している.“that could have alternative uses,” では,alternative uses をあきらめるという opportunity cost の代償をはらってまでも選択する, という内容が素直に伝わるのに, これを,「代替的用途を持つ」 と訳しては,その前の誤訳「現在および将来」との相乗効果で, その内容は (原文に何が書いてあるのかをあらかじめ予想できるのでなければ) 絶対に伝わらないだろう (翻訳した人はこの副文が仮定法で書かれていることすら気がつかなかったのではないか). たった一文なのに,翻訳の不備や日本語の破綻については,まだいくらでも言えそうである.
上の日本語訳のスライドのページを書いた人は,ネットで見ると, 日本語でしか論文を発表していないようなので, 経済学を,上で引用したスライドのページあるような,頭痛がしてくるような日本語で勉強した可能性が高い. この人が出典を間違って挙げていること (Samuelson の 1948年の本に,上の翻訳に対応する経済学の定義が載っていないことも, 全文検索して確かめた) は,ことさら,この可能性を強く示唆するもののように思える.
しかし,このような 「間違った」日本語を受け入れて, 経済学の勉強を続けて大学の先生にまでなれる感性 (の欠落 ?) ないし日本語力 (の欠落 ?) を持った人が, 何か筋の通った議論を (日本語で) することが,そもそもできるものなのだろうか ?
私は日本の 「専門家」に対して大きな不審を抱くものであるが, 上の訳文を挙げているスライドのページ (をネットにあげている,このスライドの著者の存在) は, この不審の正当性の裏付けの一つになっているような気がする.
ある (自称?)「専門家」の発言をネットからひろってみると,
「もし、3つの予防法を突破してウイルスがお口の中に侵入したとします。 そうすると、これらのウイルスは舌や喉で増殖していよいよ体内に入り込むことになります。 これから後のステージで大事なのは、舌に停滞するウイルスや細菌を舌ブラシで除去することと、 歯垢を徹底的に除去することになります。直接的には舌を綺麗にすることで、それより先にウイルスが侵入するのを防ぎます。」 (http://tetsugakudo.com/blog/1261/)
似たような発言が複数見られたのだが, この人たちはヴィルスが何だか全然分っていないのではないか?
ヴィルスは,生物のように 自律的に自己増殖できるわけではない. 細胞の中で,細胞の自己増殖の機構を借りて増殖するだけである. したがって,ヴィルスが 「舌や喉で増殖して」いるときには,これは舌や喉の表面で増殖しているのではなく, 既に細胞たちの中に入っていて,複数の細胞内で増殖して,増殖した結果としての伝播のための形態のものを 「舌や喉の表面」に細胞たちから放出していることでしかありえあない. うがい薬がヴィルスを不活性化できるとしても (この場合ヴィールスは生物でないので, 「ヴィールスを殺す」とはいずれにしても言えない), これは,このようにして感染した細胞たちの外に放出されたもののみなので, 細胞たちの中で増殖を続けているヴィールスを不活性化できるわけではない. povidon iodine などを含むうがい薬は, 咽喉の一部の細胞も殺すので,殺された細胞内で増殖活動をしていたヴィールスの不活性化はできるのかもしれないが.
ヴィールスの感染が喉から肺に移行するのを,うがいで,阻止ないし軽減できないか, ということ自体は,詳しく検証してみる価値はあるかもしれない.しかし,ここで言ったことから, 仮に効果があるとしても, 効果を出すにはかなり連続的にうがいを続けなくてはならいように思えるので, そのためには,うがい薬は強すぎるのではないかと思う.たとえば, 「いそじん」で頻繁にうがいをしたときに,色々な負の効果が出ることは, 耳鼻咽喉が炎症をおこしやすくて,日頃うがいをよくしている人は,皆, 経験として理解していることだと思う.
逆に,うがいが肺への感染の遅延の効果があるなら, 体が抗体を作り出すなどの対策をとれるための時間かせぎができるので, 重症化の阻止ができなくはないかもしれない.
一方,喉の深い部分でうがいをしたときには,誤嚥の危険があり, これは高齢者ではかなり深刻な危険となるようである. ちなみに誤嚥とは,この場合,うがいの水を気管から肺の中に入れてしまうことであるが, うがいをしていると,ついこの誤嚥の危険ぎりぎりのところまでやってしまいがちなので, 高齢者になっていることに気がつかないでいる私のような者は気をつけなければいけないだろう.
しかし, 一部の独裁国家に対しては,今,指摘したことは,もっとずっと手っ取り早い方策を示唆してもいる. それは重症化した患者をすべて,即刻に焼却ないし埋葬処分してしまう, という方法である.これは実際,家畜での感染病ではとられている処理方法である (家畜では, 重症化した個体どころか,症状の出た個体を含む herd 全体を処分してしまうようである). このやり方で医療体制の崩壊も免れることができるし, 重症化を起したヴィールスのヴァリアントも確実に根絶することができる.
もちろん,そのような行為を人間に対して行なうことが国際社会から許容されることはありえないから, このことは,あくまで秘密裏に行なわれなくてはならず, それができるだけの組織力を持っている,独裁,ないし準独裁国家の数は限られている. 地理的に,日本から遠くない国で,それが行なわれているかもしれない/行なわれていもおかしくない, と思える場所がいくつかあることは,気掛りなことではある.
しかし, そのような方策に出るためには,本当に独裁国家である必要があるのだろうか? 経済優先を叫ぶ人たちにとって, 家畜に対して行なう効率的な処理方法を人間に適用してはいけない, という理由は本当に見つかるのだろうか. 経済優先を叫ぶ人たちの言っているような (コロナ以前の経済システムの意味での) 経済効率に特化した経済優先は, 独裁国家であるかどうかに拘わらず,もしそれを純粋に理性的な判断の下に推し進めたときには, 重症患者の焼却処分に向うのではないだろうか?
ちなみに,これはもちろん 「経済優先を叫ぶ人たちの言っているような経済効率に特化した経済優先」が間違っていて, 「理性的な判断」が間違っているのではないのだが,こういう議論をすると, 「理性的な判断」が悪いと勘違いしてしまう人が沢山いるのではないかと思う. 困ったことである.
マルサスの人口論 (Thomas Robert Malthus, An Essay on the Principle of Population, 1798) で人口の増加は “increasing at a geometrical ratio while an increase in food production was limited to an arithmetic ratio” であると言われていて [wikipedia], この “幾何学的増加比” というのが “比率をもとにした” というような意味合いで使われていたものであることがわかる. この “geometrical” と “arithmetic” は,現代では,それぞれ,「指数関数的」 (exponential) 「線型」 (linear) と表現される.線形性の概念が「線型」という用語で議論されるようになるのは, マルサスより後のことなので,マルサスが線型という言葉を使っていなくても不思議はないが, 日本での多くの分野では, マルサスの時代の用語と現代の用語の対応が理解されずにマルサスの表現が現在でも継承されていることがあるようである. 試みに和英辞典を見てみると, 「幾何級数的」に対して geometric というような,使えない訳語しか出てこない.
指数関数的な増加が議論されることが多いのは,現実世界での 「爆発的な」増加が,連鎖反応によって惹き起こされることがほとんどだからだろう. 原子炉の制御も, 人口爆発の抑制も, コロナヴィールスの感染拡大の防止も, 連鎖反応による指数関数的増加の阻止という同じ問題の異る実現にすぎない. 爆発的な感染拡大ない で,それを書いた時点での日本の 「感染対策」に対して言った皮肉は, もちろんこの類似性を念頭に置いた発言である. しかし,このような類似性を本質的な同一性として認識できる,というのは, 割合高度な知的活動に属すことのようである. 「工学系」と呼ばれる人達の過半数がこの種類の同一性を認識することができない, という事実は,日本に移住して以来, この20数年ほどの間,日本の地方の大学の工学部の先生として過した時間の中で,同僚の先生方から学んだことの一つである.
大学の先生でも認識がきわめて難しいことが,一般の人々にとって認識できない, というのはある意味自然なことかもしれないが,実際には,もっと恐しい状況が起っているようである. 昨日 (20.07.25(土)) 日本のニュース報道で, 小池都知事が,CVID-19 の感染拡大に関連して使った「幾何級数的」な増加, という言葉がわからない,といういちゃもんをつけた人の話があったが, 「一般」の石器時代人は, 本質の認識ができない, ということに留まらず,彼等の語彙にない,本質を語るために必要なる単語を使うこと自体が, 彼等にとっては,すでに彼等の世界に対する冒涜になる,ということのようである.この人は,この言葉の説明を聞いて 「それなら,倍々とか言えばいいじゃないですか」と不満をぶちまけた,ということである.
実は,線形な増加と指数関数的増加の差は,単にこの2つの種類の増加の違い, ということに留まらない, もっと大きなものである.すべての多項式で表される関数より指数関数の方が速く増加する, ということが言えるからである. これは微積1 の知識があれば,多項式の次数に関する帰納法で証明できる.たとえば, 物理現象には,線型に近似できなくても二次関数では近似のできるようなものが多く存在するが, そのようなものの増加のパターンも指数関数に比べればマイルドな増加でしかない.
指数関数的な増加が,究極の増加なのか,と言うと,そんなことは全然なくて, たとえば,階乗関数 (factorial functions) の増加は指数関数の増加を超越するものになっている. 階乗関数は,場合の組合せの数の計算に出てくる関数なので, この関数が指数関数をも超越する増加の度合を持っていることは,大数の法則や, 情報量の爆発, といった現象に寄与するものとなっている.
実は, ここに書いたことを書き始めたきっかけは, 今受けもっている線型代数の online 講義で,determinant の定義にからんで,$n$ 次の対称群 $S_n$ の要素の数は $n!$ である, というような話をしたことだった. $n$-次正方行列の determinant は,$\sigma\in S_n$ の一つ一つについて $\sigma$ の偶奇性と $\sigma$ で制御される添字を持つ行列の $n$ 個の成分の積を考え, これら $n!$ 個の,積からなる項の和として定義される. この定義にそって実際に計算しようとすると,$n!$ の増大の呪縛のために, $n$ がちょっと大きくなると現実的には計算は不可能になってしまう. このことを理解するためには,$n!$ の増加の度合についての理解が必要になるわけである.
線型な増加と指数関数的増加は,経済学では,単利と複利という言葉で説明される. 経済学の人々の間では, アインシュタインが「複利は世界の八番目の不思議である」と言ったということになっているらしい. ほかの引用では,彼は「複利は宇宙で最強の力である」と言ったということになっている. アインシュタインは指数関数的な増加について 「一般の人」に話すときの喩えとして,何かの機会に,複利という言葉を使って説明したのではないだろうか.そして, 経済学の人たちは月を指した指を見て,これが金利の話だと思い込んでしまった, というのがありそうな話であるように思える. この月を指した指を見る,ということでは「倍々」と「複利」のどちらがましかは, なかなか微妙な問題かもしれない.
最近,よく 話題にのぼるビックデータは, この階乗関数のパワー (に対抗するためのコンピュータの力づくの利用) である. 経済学者にまつりあげられたアインシュタインの言葉のように,そのうち, 「ビックデータは宇宙で最強の力である」とかなんとか,有名人の誰かが言ったことにならないだろうか.
When I visited Silesia in Poland last year, there was a sign on the door of my hotel room written in Polish, English and German. The German notice read „Nach Betreten sowie beim Verlassen Zimmers bitte die Tür verschließen.“

Some of the Japanese phrases cited in the article remembered me this strange German sentence. In the following, I would like to mention just two of them.
アメリカで抗議していた人々と団結する: This sounds like the people in America referred in the phrase already stopped their protest. If the protest in America is still on-going, the phrase should be アメリカで抗議している人々と団結する.
黒人の命が尊重されていない限り全ての人の命が尊重されていない: There are one grammatical error (with 助詞) and a couple of semantic errors in this sentence. A correct sentence would be: 黒人の命が尊重されない限り全ての人の命は尊重されない.or 黒人の命が尊重さ れない限り全ての人の命も尊重されない.The construction
“aaa が bbb ない限り, xxx (*) yyy”
sound only natural (or even grammatically correct) if (*) is “は” or “も”. In case of “も”, the meaning of “also” will be attached to the “xxx (**) yyy” part of the sentence. (*) simply cannot be “が”. Similar thing happens, for example, if you say あなたが行くなら,私は帰ります. This sentence can never be formulated as あなたが行くなら,私が帰ります.
In contrast, あなたが行かないなら,私が行きます is correct! The explanation for this would be too long to be formulated here. A simplified explanation for the last example would be that the second “が” is correct since it emphasizes 私 in contrast to あなた for the same action 行く.However あなたが行くなら,私が行きません. is again wrong. The sentence must be あなたが行くなら,私は行きません.
If the sentence in the article would be modified to the grammatically correct 黒人の命が尊重されていない限り全ての人の命は尊重されていない, it might not be a wrong sentence anymore but it would mean something like “Unless the lives of black people have not been respected, lives of all people would not have been respected.” The strangeness you detect in this Japanese sentence is, I think, because the construct in Japanese language corresponding to past or perfect tense in English has more tendency to express not a conclusion of a causal expression with certain hypothetical character but rather an established fact.
I am quite curious to know who composed all these slogans.
The following example was not included in my original comments. However, I think, it represents a quite interesting aspect of modern (mis)usage of Japanese language.
The two Japanese sentences above taken from “The language of Black Lives Matter in Japanese” might be composed by a non-native speaker of Japanese. The following nominal clause can be an invention of a native speaker. I set the language of the operating system of my Mac to English, because, in the setting of Japanese language, I would be exposed to terrible Japanese translations of technical terms. The terribleness is quite of similar kind as with the following example which is also taken from the same article. Of course, the correctness of the sentence above is a semantic matter: In a sentence, which express timeless mathematical trueth and with the causuality, which is the mathematical implicateion, I would say, for example, $2=3$ が成り立っていないかぎり,$4=4$ は成り立たない. This sentence is correct and natural Japanese sensence which is also logically correct. In a lecture on logic, I would mention something more provocative like $2=3$ が成り立っていないかぎり, あなたは人間でない as an example of true sentence.
The naturalness of the last two examples is rather ristricted. Perhaps, they are natural only inside a mathematical discussion.
制度的人種差別: The problem of this compound word is of course purely of semantic nature. The prolem here is that the adjective 制度的 has too much positive connotation reflecting the strongly obedient attitude of the average of Japanese people. It could be back-translated as something like “according to the well-established (nice) rules” although there is also a compound word as “奴隷制度” (slavery, perhaps this Japanese word was coined in this way at the time when slavery was still one of the possible options). However, since the phrase should refer rather something which happened to be fixed in a system in a wrong way, and since, on the other hand, too much subjective, negative connotation shoould not be attached to the expression, my suggested translation would be 構造的人種差別. “構造的” is a big word and it might suggest too much the structuralism in the sense of mathematics or philosophy. Still, I think, it is neutral enough to be used in this context.
英語とドイツ語の wikipedia を含めたネット上の情報によると, トランプ大統領の祖父はスペイン風邪で 1918年の5月に亡くなっているらしい.
悲劇的な死をとげた人の家族には,そのトラウマがゆがんだ形で残ることが多い. たとえば,私の母方の祖父母は, 一番上の2人の子供を疫痢で失なっている.このトラウマは私の母に受けつがれたようである. 私は子供の頃に体が極度に弱かったので,生き残れたのは,一重に私の母のおかげであるが, 今思い出してみると, 母の私の健康に対する対策の中には,この祖父母のトラウマから由来していると思われる, 理性的というより呪術的なものが沢山交じっていたようにも思われる.
トランプ大統領の COVID-19 に対する対応も,やはり,死んだ人の家族に残されたトラウマのなせる業なのではないだろうか. たとえば,彼はこのトラウマの由縁から COVID-19 で死んでしまうことに対して大きな恐怖心を持っていて, マスクを絶対にしない,というのは,彼なりの COVID-19 への宣戦布告の呪文なのではないだろうか. 呪文という観点からは,この仮説は,彼の最近の演説での Kung-Flu 発言も非常にうまく説明できるように思える.
また,ここで言った仮説は,5月にトランプ大統領が 5月にhydroxychloroquine を摂取していると報道陣に話したことや,消毒薬を飲めば COVID-19 が治るのではないかという発言とも噛み合うし, CNN が最近報道した, トランプ大統領がコロナビールスに罹らないよう, 遊説先での彼の使うトイレの徹底的な消毒をはじめとした,様々な対策を指示している という,トランプ大統領の言うであろうところの “fake news” ともうまく噛み合う.
トランプの不思議は,彼の信奉者たちの不思議にもつながる.テレビのインタヴューを見ていると, 黒人やラッティーノズの,彼の信奉者のインタヴューが頻繁に出てくる. これは “フェイクニュース” の, 人がびっくりすることをことさらに取り上げようとする傾向からのチョイスなのかもしれないが, 人類の「差別」の歴史で起こったことを見渡して考えてみると,この人たちは,トランプ大統領を支持することで, (トランプ大統領を支持するような) 白人の側に越境できると思い込んでいるのではないか? というが, 自然な推測であるように思えてくる. これと正反対の行動に出るには,いささかの心の余裕や教養が必要になるかもしれない. Caroline Randall Williams の この論説も参照されたい.
また,前に言った呪文ということで言えば,トランプ大統領の信奉者たちは,呪術師のそれのようなものかもしれない. カリスマという呪術を使う「政治家」と呪術という政治を行なう「呪術師」は,いずれにしても同義語なのかもしれないが. 石器時代人からなる大衆を動かすのは,自分自身が石器時代人であるか, 石器時代人のふりのできる人であるかでしかないだろう.
例えば,ドイツの政治システムでは,大統領は,ほとんど政治的な実行権はなく, 平たく言うと,その主な役割は „volksnahʺ であることである,と説明されるが, この„volksnahʺ はもちろん 「自分自身が石器時代人であるか, そうでないとしても石器時代人のふりをすることができる人」であるか,ということの Euphemismus でしかない. 日本でも,日本の象徴であるところの天皇と内閣総理大臣との間で, ドイツと似たような役割分担ができてもよさそうにも思えるのだが,日本の場合は, 内閣総理大臣が,石器時代人と同等の知性を発揮することで,民衆の賛同, または,賛同とまではいかなくても,民衆の安心感を惹き起こす, という政治のメカニックスができあがってしまっているので, たとえば,本物の理論物理学の学位を持っている人物が総理大臣に就任する, なんていうことは金輪際ありえないだろう.
アメリカやヨーロッパでは, コントロール欲のかたまりの政治家の暴走をおさえる魔法の言葉として,多分, Severn Cullis-Suzuki が最初に言って Greta Thunberg の広めた 「 scientists の意見を聞くように」,というのがあるが,日本で意見をうかがうべき人達として出てくるのは 「専門家」なる非常に怪しい人たちで,しかも,「専門家の判断を仰いで」と言うときには, この「専門家」(多くの場合,無名で日本語の特性から複数なのか単数なのかも分らない) が,どういう rational からその判断に至ったのかを説明することは (あるいは説明ができることは?) 全くない, という非常に危ない状況が定常化している.「有識者」という言葉もあるが, これは言葉のニュアンスから scientists を除外すらしているように思われる.
この文章は, 今「大阪モデル」なるものが, 大阪府で決議され, 神戸がそれの真似のような規則を導入しようとしている, という現在 (20.05.15(金14:58(JST))) の状況を背景に書いているものだが, 実は,私が今神戸大学で始めているインターネット講義での線形代数のクラスにつての経験も頭をかすめている.
講義を機能させるために, 宿題のネットでの提出の期限や提出の方法や宿題のファイルのフォーマットなど色々ルールを導入しなくてはならない. 教師は講義についての絶対的な権限を持っているので, ルールの設定はもしその気になればやり放題である. 髪の色やパンツの色まで指定しているという, 日本に実存するらしい多くの女子校の校則のようなものまで導入できてしまうかもしれないし, そこまでいかなくても,たとえば,もし日本にもそういうものがあれば, 「レポートの記述は MLA format に従うこと」というようなルールまで導入してしまうかもしれない.
インターネット講義に必要なルールを,講義システム (神戸では,Moodle の一つの instance を教育システムとして導入してあり,これを使っている) で受講者にアナウンスしているとき, ひょっとしてこれは単に僕の他人をコントロールしたい欲望を満たすための行動になっていないだろうか? という不安が頭をよぎるのである. 一つ一つのルールは学生が対応しやすいことや,少なくとも教育効果と共存するものになっていることや, 私が作業をしやすいこと,などを勘案して慎重に決めているつもりではあるのだが.
今年の3月ごろ,まだマスクの使用について国際的には否定的な意見が強かったころ,New York の地下鉄の駅でマスクをした東洋人の女性が黒人の若者たちに暴行される映像が出まわったことがあった. この映像は,ひどく不思議に思えたが,後になって,文脈が分って納得することができた.
アメリカで,マスクをする義務が導入されたときに,黒人のコミュニティーが, マスクをすることで嫌疑をかけられて白人に射殺されることの方が COVID-19 に感染することより恐い,というステートメントを出した.実際, ランニングをしていた黒人が白人に射殺される,という事件が最近 Georgia で起こり, 事件が適切に処理されなかったことがスキャンダルになったりしているので, この心配は,被害妄想などでは全くない. このステートメントに関する記事を見て先程言った映像の意味がやっと理解できた.
アメリカの黒人の子供たちは, 顔をかくすなど, 白人に嫌疑をかけられて射殺されるかもしれない行動を絶対にしないよう,小さいときからきびしく教育されているにちがいない. マスクをした女性を襲った黒人の若者たちは,この教育を素直に受けて育ち,マスクで顔をかくすという 「悪」に「正しく」反応したのだろう.
マスクの文化的な conotations の違いは面白いものがある.月光仮面, 鞍馬天狗など,日本では正義の味方が口を覆うマスクをしていることが多いのに対し, アメリカ映画を見てみると,Darth Vader をはじめ,face mask をしているのは圧倒的に悪者だし, 正義の味方がマスクをしているときには, ほとんど例外なくカーニバルの仮装のような目の回りだけをかくすマスクである. これは,黒人に嫌疑をかけて射殺してしまう白人の側の背景になっているのだろうし, ブルカを極端にいやがるアメリカやヨーロッパの文化的背景でもあろう.
[この項はまだ書きかけです]
それにもかかわらず,これが,もし無限大数が一,僕に起こってしまったとしたら, 僕はそれを幸運と思って死んでゆくべきなのだろうか? それとも, それを臨死の幻想かと疑いながら死んでゆくべきなのだろうか?
誰もできないでいた「すごい」ことを自分の国の誰かが成し遂げた, ということを自慢に思いたがる人,というのは,ひどく滑稽だが, そういう心の動きをする人が (日本に限らず世界中に) 沢山いるらしい, というのは面白い現象ではある. 数学者なら,同じ日本の劣悪な研究環境の中で,すばらしい研究成果をあげた, ということが心のはげみになる,ということならありえるかもしれないが, 望月氏の場合,彼はアメリカ産の数学者だし,現在は数理研教授という特権を亨受されているので, そういう意味での日本の平均的な数学者の心のはげみにはなりにくいだろう. むしろこれを誇りに思いたがっているのは, 数学について何も知らないし知ろうともしない人たちだろう. そして,日本のメディアがアピールしたがっているのは,まさに,この数学とは関係のない人たちの, 「同朋」の 「快挙」を自慢にしたいという,滑稽きわまりない欲求そのものなのではないだろうか. これは,日本の演奏家の誰々が国際音楽コンクールで優勝しました, というニュースや (この場合,コンクールでこの演奏家が演奏したのが何でそれをどう演奏したのかは全く報道されないことが多い), 日本の運動選手が外国の大会で優勝しました, というようなニュース (この場合には, 驚くことに,スポーツの種目が何だったかは報道されることが多い) などと全く同じ種類の現象なのだと思う.
abc 予想は,その命題から,数論での大きな予想やフェルマーの大定理のように既に証明の得られている定理などが, 多くの場合,初等算術的な議論で,導けてしまうので, その証明が得られると,それは数論のパースペクティヴを根底から変えてしまうことになる. この意味で abc 予想は,それが難しい問題であるかかどうかを越えた重要度を持つ問題である. フェルマーの定理が Peano arithmetic で証明されると予想されているのに対し,abc 予想は,ある fast growing function の存在を帰結する可能性があり, そうだとすると,これが証明できているのなら,それが,集合論では証明できるが Peano arithmetic では証明できない,という Paris-Harrington タイプの命題の,新しい数学的な例になっている,という可能性もあるのではないかと考えられる. ちなみに,フェルマーの定理と同様に, 不完全性定理の証明でも用いられるコーディングのテクニックを使うと,abc 予想の命題も Peano arithmetic で単一の closed formula として表現することができることは容易に理解できる.
数学の正しい証明は誰でも理解できる. もちろんこの場合の 「誰でも」は思考のリソースが足りないためについてこられない人は切って捨てた後の 「誰でも」ではあるが. 実際には,少数の例外的な天才 (つまり全人類の歴史の全体の中での数十人程度) を除くと, 誰でも思考のリソースは不足気味なので, 「理解できる」というのは,多大な努力の末の理解となることが多い.しかし,数学の理論は,一旦理解してしまえば, 全景を一望に見渡せるようになることが多く,この「全景を一望に見渡せる」という快感のために, 大抵はくそ分りにくい書き方をしているところの他人の論文を,我慢して苦しい思いをしながら読むことになるのだ.
望月新一氏の証明が正しいかどうか, という問題は,だから, 個々の数学者にとっては, 最終的には彼/彼女がその証明を自分自身で理解して全景を一望に見渡せるようになれるか, あるいは,多くの場合これと同値な命題になるのだが, 彼/彼女が自分のための別証明を作り出すことができるかどうか,というような問題にすぎない. 逆に,自分の現在の研究から遠い分野の数学的結果を精査するだけの余裕のない僕にとっては, この abc 予想の証明の真偽は,上で言った数理論理学からの興味にもかかわらず, 今のところ自分で手 (と頭) を動かしてみることの, できない,あるいは,それをすることの予定の作りづらい問題になっていて,だから, これについてはとりあえずこれ以上何も言えないし,言うつもりもない.
ただ,ひとつ気がかりなのは, 望月氏の結果をしきりに日本のメディアでもちあげているらしい人が, かつて,数理論理学について間違った,というかまったくデタラメなことを沢山書いていて, その訂正を今もって全く何もしていない, ということである.この人が 「正しい証明はありまぁす」と言っている,ということのうさんくささが僕の嫌疑をかきたて,心の平静を乱している.
とりあえず自分のことは棚に上げて,周りの数学者たちを見回してみると,この楽観性は, 思い込みの激しさから来ていることが多いように思える. あるいは楽観的でいられるのに必要なほどの思い込みをする能力がある,と表現すべきか. もちろん生産的な数学者であり続けるには,思い込みで暴走するだけではだめで, この思い込みから,ある瞬間には抜け出ることもできる柔軟性も兼ね備えていなければならないだろう. そして,この思い込みから脱出することができる柔軟性,という有能な数学者の高度な能力は, ある場合には,他人の思い込みの激しさを指摘せずにはいられない,という衝動としても発揮されるようである.
昨年89歳で亡くなった志村五郎は,その生涯を現役の数学者として貫いた尊敬すべき先人である. 彼が書いたものの中に見られるコメントには, 数理論理学に関する否定的な意見や数理論理学に関する彼の無知を露呈するものもいくつかあるので, 私の研究の同僚の中には彼のことを否定的に言う人もいるのだが. ちなみに,数学では無知であることは固定観念に足をひっぱられないための非常に有効な財産であるが, これは思い込みと組み合わさったときには大変に醜い結果を産むこともある危険な状態でもある. 志村先生の場合, 数理論理学に関する無知は, 「ロジックは三流の数学者がやることである」というような思い込みと組み合わさって醜い結果を産んでいたように思える.
その志村先生が晩年に執筆された自伝 「記憶の切繪図」,「鳥のように」また,「記憶の切繪図」の(ある意味での) 英語版である "The map of my life" には, 「誰々が何々という単語を是之と発音したが正しい発音は之是である」というパターンの指摘がいくつも出てくる. その中の一つに,政治学者の丸山眞男が Thomas Mann 夫人の名前 Katia を 「カーチャ」と発音しているがこれは正しくは 「カツィアでなければならない」というのがある. 丸山眞男に関しては,志村五郎の本には,丸山が色々な思い込みからいかに自由になれなかったか,という逸話が延々と書かれていて, これはその中の一つのエピソードである. でもこれは,少なくともドイツ語で発音したもののカタカナ近似ということなら, 正しいのはむしろ「カティア」である.僕より上の世代の日本人で「チ」「ツィ」「ティ」 「チュ」等の区別のできない人は少なくないと思われるので,これを責めるのは不適切とは思うが, 他人の思い込みを指摘して自分の思い込みが露見してしまう, という数学者にありがちな喜劇的な状況については,指摘しておいてもいいように思えるのである. ちなみに,僕の「カティア」説自身が思い込みではないか, という人もいるかもしれないが,僕はそんなことは絶対にないと思う.
なにしろ Katja Riemann のファンの僕が言っているんだから.
一方,今日になって,大阪市市長は花見の自粛を要請した.
The person added the “graffiti” is a genius!! If this person is Bankcy himself, I can respect him a little bit. But in this case, I just hope that he is not going to coming out with the fact, at least not very soon until all the stupid remarks about the “vandalism” have been made.

しかし,ナチス・ドイツの国民は,遅くとも, 連合軍のノルマンディ上陸で,秘密兵器を持っていたのは連合軍の方だったことを理解しただろうし, その秘密兵器の一つが Turing の "bomb" だったことも, ずっと後になって理解しただろう.一方,大日本帝国の国民の方も,遅くとも広島, 長崎に atomic bombs が落ちた段階で,この「新型爆弾」を含む秘密兵器を持っていたのがアメリカの方だったことを, もっと直接的な形で理解して,無条件降伏の天皇による宣言を比較的無抵抗に受け入れることができたのだろう.
広島と長崎への原爆の投下をめぐる議論,歴史解釈では, アメリカ側でよくなされる (Truman 大統領の原爆投下後の声明にもある) 「戦争を速やかに終結させるには必要だった」という内容の主張や, 「アメリカが日本に原爆を投下したのは, ソビエトへの警告のためにすぎなかった」という主張など, それぞれ,もっともと思える部分も持つ主張が,異なる視点や陣営からなされている.
この「戦争を速やかに終結させるには必要だった」という内容の主張については, 日本の視点では, それだからといって原爆を投下して多数の儀牲者を出す必要はなかっただろう, という反論から否定的にとらえられることが多いように思える. 日本で,この主張の正当性を認めると,「アメリカ様」の手下になっている, というようにしか見られないのではないだろうか. しかし,日本側でなされることの多い,この反論は, 日本で,アメリカによる旧来の爆弾や焼夷弾によって, 原爆で犠牲になった人の数よりずっと多くの人が亡くなっていること (原爆のために, 世界ではこのことを全く知らない人が多い --- ただし無差別爆撃に近い形の爆撃を最初に始めたのは, アメリカではなく,多分,ドイツであろうが ... --- だからもしこの議論をするなら, 旧来の爆撃に対する批判から (しかもアメリカの日本への爆撃に限定せず Dresden の爆撃なども含めて) 始めるべきである) や, 日本側が「国体」という共同幻影 (?) のために自国民や当時に統治/植民地化していた土地や地方の人々を犠牲にしたこと, など,多くの他の事実やファクターを全部帳消しにする形でなされていることが多く, この「戦争を速やかに終結させるには必要だった」の類のことが主張される多くの場合と同様に, 議論以前の議論の文脈での発言であることが多いように思える.
[20.07.05(日09:09(JST)) の補筆]: 実は,この post を書いた後で これに更に書き加えようと思っていた話は,神戸大学の広報から要請されて書いた 「定年退職にあたって」という作文 に既に書いてしまったので,そちらを参照されたい.
この場合, 人類の絶滅の,恐竜のそれとの違いは, 恐竜たちが,多分,彼等の絶滅の運命を全く予知できなかったのに対し, 人類は自分たちに起ることをかなりの精度で予測できることになるだろう,ということだろう. ただし,この予測を人類のうちの多勢が直視できることになるかどうかは,また別の問題かもしれないが.
これから必然的に起ることになる地球温暖化の末の人類の絶滅は, これとは違う,もっとずっとぶざまな終りになるだろう. これに関しては, (今の時点ではまだ) 対策はとれるかもしれないし, それを人類の知性は理解できるし理解もしているはずなのだが, それに対する可能な策が,すべて人類の習性の適応範囲の外にしかないために, 何もできずに終ってしまう,ということになるだろうからである.
これに関しては,日本のある政治家の親子のことが思い出される.この父親は「痛みを伴った」改革を行ない, 息子は,「セクシーでなくてはいけない」と言ったが, もっとセクシーでなくてはいけなかったのは,むしろ父親の行なった改革の方で, 激痛以上の痛みを伴ったものではなくては全く意味をなしえないのが, 息子の言う温暖化対策のはずなのではないだろうか.Von der Leyen 欧州委員会委員長は,少なくともこのことを正しく理解しているように思える.
--- Her dream is surely unrealistic. The humanity will become extinct
at latest (but very possibly much earlier than) in 200 years anyway. The matter here is rather if we can maintain the
dignity of the human mind at the end of the human race in the same sense
as C.Gustav Jacobi put it when he claimed in a letter
to Legendre in 1839 that the ultimate objective of mathematics is "l'honneuer de l'esprit
humain":
Il est vrai que M. Fourier avait l'opinion que le but principal des mathématiques était l'utilité publique et l'explication des phénomènes naturels; mais un philosophe comme lui aurait dû savoir que le but unique de la science, c'est l'honneuer de l'esprit humain, et que sous ce titre, une question de nombres vaut autant qu'une question du système du monde.
— C.Gstav Jacobi, 1839
さて, この記事の載った特集号を眺めてみたのだが,それでも 「巨大数」は今もってよくわからないので,代わりに「虚大数」という概念を導入してみたい.
定義. 明確な定義や計算のアルゴリズムがあるのに, それがどの数か特定が現在のところされていなかったり, (infeasible という意味で,あるいは理論的に impossible という意味で) 特定することが不可能な数を,虚大数と言うことにする. ただし,虚大数と言う場合には,その数の存在が証明されているか, その非存在の絶対的な証明の非存在が証明されているものとする.
例.
Ramsey number: 例えば,$798\leq r(10,10)\leq 23556$
Equidistance graph の chromatic number: $5\leq\chi\leq7$
PA からの矛盾の導出のゲーデル数
巨大数の多くは虚大数である.
Ramesy number は,有限的な決定方法が存在するが,たとえば $r(10,10)$ は普通に考えられるアルゴリズムでは, 物理的に可能な時間やリソースの範囲では計算できない. 多くの巨大数についても,有限的である,という点ではかわらない.Equidistance graph の chromatic number では状況は異なる.この数が決定できる (たとえば, $5$, $6$, $7$ のうちのある $n$ について ZFC で $\chi=n$ の証明ができる) かどうかすら分っていない.しかし将来, たとえば,ZFC で $\chi=6$ が証明されてしまう可能性もあり,そのときには, この数は, 虚大数ではなくなってしまう. 過去に虚大数でなくなった数としては $x^n+y^n=z^n$ が整数解を持つような最小の数 $\geq 3$ というのもある. 「PA からの矛盾の導出のゲーデル数」はもっと微妙である. この数の非存在が証明できないことは,ゲーデルの第2不完全性定理から導かれる. $0$, $1$, $2$ と順にそれらの数が 「PA からの矛盾の導出のゲーデル数」でないことを調べてゆくことはできる. このやりかたで「PA からの矛盾の導出のゲーデル数」が見つかったときには, その数をデコードすると PA が矛盾していることが示せたことになる. このことが起こらないという絶対的な保証は存在しない.
虚大数は実数でもありえる.たとえば $L$ 上の Cohen real, $0^\#$ など.
巨大数は巨大基数と関連があまりなさそうだが,
虚大数の巨大基数との関連は多層的であるように思える.
[この項は後でもう少し書き足す予定]
先日ある研究集会に参加したら,質問に答えて「自分は哲学者なので, 数学の最先端のことは勉強しきれない」というようなことを言った人がいた. この発言が哲学に対して無礼なものにならないところが,日本の「哲学」の 「日本の哲学」たるところなのだろうが, そういう「日本の哲学」の問題は別としても, こういうことを言う人がしゃしゃり出て講演をしたりするのはやめてほしい.

「樹を植える」というのは, 「世界平和」や「節約」などとは違って人類が実行できるアクションだろう. 樹を植えることは,農耕文化と同じくらいの歴史を持っているはずで,これは 『Carla Reestma』 でも触れた「貨幣経済」よりも更に古い歴史を持つものだろう. ただし,貨幣経済そのものは比較的新しくても,たとえば 貨幣経済の出発点の一つになっている人類の貴金属に対する嗜好自身は,胃石を飲みこむ, という恐竜時代より更に古い時代に DNA に組み込まれた動物の本能に根差しているわけなので,あなどることはできない.
いずれにしても,温暖化対策の有意なものの一つに,この人間にとって feasible な行動が含まれている,というのは人類の存続にとっては明るいニュースであろう. しかし,過去の 「自然保護」運動などの経緯を思い出してみると,この明るいニュースにだけ反応して, その反応を儀式化して、それでいいことにしてしまう, というのも人類が過去に何度もとってきた行動様式の一つなので, このニュースが広がること自体は人類にとっていいことなのかどうか、という疑問も残る.
植樹による CO2 対策の一番の問題は,植樹をしても育った樹木を建材にしてしまったのでは,もともこもない, ということだろう. これをすべて,例えば,何億年か後に今の (発掘前の) 化石燃料のような状態になるような形で土に返す, ということが人類にできるんだろうか,と考えるとかなり怪しい気がしてくる.
このビデオの完成度から見ると,彼女の回りには十分に有能なメディアまわりのスタッフがいるのだろう. あるいは,これはビデオで共演している George Monbiot の回りにいるスタッフなのかもしれない. 空襲警報のようなもののパロディーではじまって Koyaanisqatsi のような映像と Philip Glass もどきの音楽に移行する opening はこの種類のビデオとしてパーフェクトで, 小泉環境大臣の表現を借りれば,十分にセクシーとも言える.
一方,インターネットをサーチすると, 人類の滅亡 (2) でも触れた Suzuki や Reemstma や Thunberg などに対する negative campaigns をしているものが沢山見つかる.これらのページの論調は, 「外国人出てゆけ」コメントをまきちらしている日本の原住民の人たちの書いていることと, ほとんど同レベルである. と言うか,むしろ何にどういちゃもんをつけるかということに関して, 大きな類似性があり, これらの発言の背後には同じ種類の動物が控えていることが感じられる.
こういうコメントを見ていると,まあ, 人類がその愚鈍さゆえに滅亡する, ということなら恐竜の滅亡と同じくらい滑稽な地球の歴史の一コマにはなるかもしれない, という気もしてくる. 貨幣経済というのもよく考えてみると非常に滑稽な原始人の習性だが, 多分人類は滅亡するまでこれから離れられないだろう.
逆に, 人類を滅亡から救うためには, この貨幣経済を含めて既存の「文化」を大きく覆さなくてはならないはずなのだが, このことは,人類を救うためには, 今まで人類が経験したことのない内容と規模の革命を (多分この20年間くらいの間に) やり終えなくてはいけない, ということである.Precht は対談の中で 「既存のデモクラシーの枠内で温暖化対策は実行できると思うか? 独裁制が必要なのではないか?」 と問いていて,Reemstma はこれを否定しているが,実際のところ本当の答は,yes だろう. 気候変動に警鐘をならしている人たちに強く反対したり攻撃をしたりしている人たちは, 実は,このことを直観的に感じとって,それに対する恐怖で動いているのかもしれない. そう思って考えてみると,ハリウッドの SF 映画では, 劣悪化した環境の中でサバイヴするために独裁化している文明はつねに悪者として描かれていることに思いあたる. ついでに言えば,多くの場合,これらの映画では, 劣悪な環境の中でサバイヴしていること自体がすでに悪として描かれていて, 差別する側の意識の基本パターンを忠実に再現している.
しかし,たとえば, 統計学の初歩も理解できない人が,地球温暖化対策を含む意思決定に際して, 統計学の初歩以上を正しく理解している人と同じ一票を持つような原始的な政治システムを維持していたのでは, 人類が滅亡以外の道を進むことはありえないだろう.
対談の中で Precht の「気候運動」は“右か左か” という挑発的な質問に,Reetsuma は即座に,運動は“右か左か” というような分類を越えたものだ, と答えているが (即答は当然想定される質問への答だったからかもしれない),これは, 自分に都合の悪いものはすべて左と言って終りにしてしまう, 日本の頭の悪い大人には受け入れられない考えだろう.そう思うと, 可笑しいような悲しいような気分になる. ("connection aborted!")
アメリカが 1970年代に月着陸計画を遂行できたのは, 月面に有人飛行で着陸する,ことが目標だったからではなく,ソ連に勝つ, という "普通の"人間が理解できることが目標だったからではないか? これに対して 「気候変動」を許容範囲にとどめる,という目標は, 月面着陸と比較してももっと抽象的で, だから,このことの意味を理解できない政治的指導者が普通にいたりするわけだが, こちらの方は問題が大きすぎて 「ソ連に勝つ」に対応するような, 多くの人が理解できる程度の矮小な (あるいは人間の本能に訴える) モティヴェーションを乗せずらいように思える. このことは, 『人類の滅亡』で, 「現在普通に知りえる情報から冷静に推論すれば, 我々の普通に想像する意味での人類の滅亡という状態が遅くとも200年後くらいには出現していて, それはもうどうあがいても不可避であることが決定している, としか結論を下しようがないだろう」と書いたときの,判断の材料の一つでもある.

Loïe Fuller のダンスは YouTube の動画でも見ることができるが,僕のイマジネーションの中では, このモダンダンスの始祖の踊りは,むしろ山村暮鳥の『聖三稜玻璃』の中にある 『だんす』という詩につながって天に蹴上げられている:
だんす
山村暮鳥
あらし
あらし
しだれやなぎに光あれ
あかんぼの
へその芽
水銀歇私的利亜
はるきたり
あしうらぞ
あらしをまろめ
愛のさもわるに
烏竜茶をかなしましむるか
あらしは
天に蹴上げられ
ちなみに三稜玻璃はプリズムの意,歇私的利亜はヒステリアである.
大昔,多分中学生の頃この詩を初めて読んだときには,
「烏龍茶」はまだ日本で普及していなかったので,
長いあいだこの「烏竜茶」は僕にとって謎の飲み物だった.
上の作文は,"Logical Dilemmas" が手元になくて書いていたのだが, オフィスに戻ったときに調べてみたら,この表紙の絵は, Gödel の奥さんの Adele が Gödel と出逢ったころに出演していたナイトクラブの名前 „Der Nachtfalter“ からの連想,ということのようだ.この „Der Nachtfalter“ (夜蛾) は Fuller のダンスの名前のドイツ語訳でもあるが,ナイトクラブの名前が Fuller のダンスから来ているかどうかは不明である.ちなみに, このナイトクラブは,„Anschluss“ の時代には, スパイ映画を連想させるような,あぶないクラブをよそおって外国人要人をさそう Gestapo の諜報のためのあやしい場所になっていたらしい. 現在では werk x-petersplatz という (前衛?) 劇場になっている (これは日本だと下北沢かどこかにあるかもしれない,政治的に engagé な劇場のようである).
「普通の数学」のほとんどの部分は Zermelo の集合論の中に展開できるので, $\omega_1$ がどのくらい「普通の数学」での考察の対象と看倣せるのか, というのは興味深い問題であるように思える.たとえば,Borel determinacy の証明には $\omega_1$ が必要になるので, Borel determinay を普通の数学に属す定理と考えるなら, $\omega_1$ も普通の数学の対象と考えなくてはいけないだろう.
こんなのはどうだろうか.次の定理の (1) は (超限) 帰納法により簡単に示せる. 学部生むけの演習問題である --- これは可算選択公理を仮定した Zermelo の集合論で示せる:
定理 1.
(1) 任意の可算整列順序は $(\mathbb{R},\leq)$ に順序同型で連続に埋め込める.
(2) 非可算な整列順序は $(\mathbb{R},\leq)$ には順序同型に埋め込めない.
この定理から,
系 2. $\omega_1$ は $(\mathbb{R},\leq)$ に順序同型に埋め込めない最初の整列順序の順序型である.
ということがわかる.もちろん系2が意味を持つためには, $\omega_1$ の存在が保証されなくてはいけないので, そのような保証を与えることのできる集合論で議論をする必要がある.
この系を $\omega_1$ が普通の数学の対象である, という主張を裏付ける命題の一つ,と考えることはできないだろうか?
逆に「すべての順序数は $\mathbb{R}$ に順序同型に埋め込める」という主張を Zermelo の集合論に付け加えた体系は (ZF が無矛盾なら) 無矛盾である. 上の定理から,これは「すべての順序数は可算である」ということと同値である. 非可算な整列順序は Zermelo の集合論でも存在するので,この「公理」は, 順序数が整列順序の代表元の系にならない, というあまりよろしくない状況を導くものになってしまっている.
付記. 上で「学部生むけの演習問題である」と書いたし, 実際,平均的な学部生にとって十分に証明の再現が可能な問題だと思うが, よく考えてみたら, 定理 1 の (1) の証明には可算選択公理が必要だが, (2) は選択公理なしで証明できることがわかった. この,選択公理がどのくらい必要になるのか,ということは扱っている主張が 「普通の数学の定理」とみなせるか,という設問とも密接に関連してくるので, 念のため証明を書き出してみた. このノートの "Is $\omega_1$ an object in the conventional mathematics?" という題の節を参照されたい.
"$<\aleph_2$" あるいは "$<$連続体濃度" を反映基数として持つ強い反映原理が成り立つことを仮定すると, 連続体濃度は $\aleph_1$ か,あるいは $\aleph_2$ か,あるいは非常に大きなものになる
というのが結論の一つで,さらに,これらのそれぞれの反映原理を導く generic large cardinal の存在公理が一様なやりかたで導入できる.
ということが上の trichotomy をサポートする定理として述べられている.言わば, "mathematical plenitudinous Platonism" の視点からの連続体仮説の解決としての trichotomy theorems である.上にも書いたように,この論文は竹内外史先生の追悼国際学会に投稿した論文なので, 結語で,私を含め, 私の世代の日本人のロジシャンがいかに竹内先生の書かれたものからインスパイアされたか, ということや,竹内先生の連続体問題への貢献についても触れている. 竹内先生が 【新版】ゲーデル (日本評論社,1998) で触れている 1970年のゲーデルの連続体仮説の "解決" についても言及していて, そこに書くことに関連した1970年以降のゲーデルに関する事実を確認するために,ネット上でアクセスできる Oskar Morgenstern の日記 を読んだ.
この日記の 1970年台後半の記載では, ゲーデルとモルゲンシュテルンがゆっくりと死に向ってゆく様子が読みとれて --- Morgenstern は Gödel の死 (1978年1月14日) より少し前の1977年7月26日に癌で亡くなっている --- かなり気が重くなった. しかし,あるいはそれゆえ,引きよせられるようにして集中して読んでしまった. 日記の記載によれば,Morgenstern が状況をかなり客観的に見ているのに対し, Gödel は自分の病状に気をとられて Morgenstern も死の病に犯されていることに全く気がついていない. もちろんこの日記にはこのことの記載はありようはないが, Dawson によると,Gödel は Morgenstern の 死の数時間後に, それを知らずに Morgenstern と話をしようとして彼の家に電話をかけて, 彼の死を知らされてショックのあまり何も言わずに電話を切ってしまったという.
これは,logically correct な statement だろう. 「すべての種族は滅亡する」「人類は種族である」ゆえに「人類は滅亡する」.もちろん, この推論の結論「人類は滅亡する」の semantical correctness は,推論の前提として用いている 「すべての種族は滅亡する」と「人類は種族である」の semantical correctness に依存する.しかし semantics ということで言えば,例えば 「人類の滅亡」と「世界の終り」は同じものなのか? あるいは「「私」の終り」がすでに 「世界の終り」なのではないか? あるいは,現代科学としての宇宙学の意味での 「宇宙の終り」を 「世界の終り」と考えていいのか? など, 確定的な議論を始められる前に確認しておかなくてはいけないことが多すぎる.
多くの政治や経済関係者(?)の発言を聞いていると,彼等にとっての「人類の滅亡」は この「「私」の終り」イコール世界の終り,という世界観に限りなく近いもののように思える.つまり, 「私」が終ってしまえば「人類の滅亡」の問題も終ってしまうので, そんなことは考える必要がない,というようなことなのではないかと思う.
我々は「私」の終りにさえちゃんと向きあえないのだから, 人類の滅亡にちゃんと向きあえないのは, 何の不思議でもない.しかし, (仮に「私」の終りの後にも世界が存在するという世界像で考えるとして) 現在普通に知りえる情報から冷静に推論すれば, 我々の普通に想像する意味での人類の滅亡という状態が遅くとも200年後くらいには出現していて, それはもうどうあがいても不可避であることが決定している,としか結論を下しようがないだろう. Stephen Hawking が生前に言っていたように人類が宇宙に進出することで, 滅亡をまぬがれる,というシナリオも可能かもしれない.そうだとしても,K-Pg boundary の後の齧歯類たちが,多分,今の人類を自分たちの子孫とはみなさないだろうように, 宇宙に進出して変化をとげた生物を,現在の我々が人類の子孫とみなせるかどうかははなはだ疑わしいようにも思える.
この200年後というのはなかなか微妙な数字である. 仮に,人類がどうあがいても存続できないというような環境条件が地球上で成立するのが200年後だとしても, 過去のいくつもの文明たちが微細な気象変動に反応して行動した結果滅亡再興を繰り返してきたことを考えると, 200年よりもっとずっと前に,気象環境の悪化が引き金になって人類が自ら滅亡の道を走りぬける, というシナリオも十分にありそうに思える. しかし,そうだとすると,人類の滅亡の直前に,それを目撃することなく, 「私」が終ってしまう,という実に間のぬけた状況が起ってしまうとになり,これは,なんとも残念としか言いようがない. あるいは,今まだ見えてきていない加速が起ることで,人類の滅亡に立ち会える光栄の可能性が, 私にはまだ残されているのだろうか?
Martin Luther が言ったと言われている 「私は明日世界が終ることが分っていても今日林檎の樹を植えるだろう」という言葉があるが, Greta Thunberg の報道を見ていると, 彼女のやっていることは, この明日の世界の終りを前にした植樹のようなものなのではないだろうか,とも思う. 樹を植えるのは尊いことだろう. 彼女のやっていることは人類の理性の尊厳に対する最大の敬礼の一つとは言えるだろう.
音は こまくの 絃琴の せんりつ の うずまき の ひばりの 舌の ひ かり り いとなっている. これは音と光の共感覚的 (synaesthetic) な,ほとんどメシアン的な表徴だった. この『数学』という詩は, 多分西脇順三郎と交流のあった数学者のことが書かれているのだが, 新倉 俊一著 『西脇順三郎全詩引喩集成』には「慶応大学教授」とあるだけで誰だったのか分らない.
二年前に Katowice で forcing の入門の講義をしたときに,この ${\cal H}(\kappa)$ を扱った講義の回に,${\cal H}(\kappa)$ の内的な特徴付けを与えようと思ったのだが (このときの 講義録 ), うまく見つからなくて,結局時間ぎれになって,この計画を放棄してしまったことがあった. 最近,Grothendieck universe (グロタンディエク宇宙) のことを整理していたら, regular な $\kappa$ に対する,${\cal H}(\kappa)$ が,僕が weakly Grothendieck と命名した,グロタンディエク宇宙の定義の条件を弱めて得られる概念で特徴づけられることが分った. これは,このノート の "Hilbert's Paradox and Grothendieck universe" という題の章にまとめてある.
Op.67 と Op.68に含まれる若い頃の作品は,ショパンの最初のマズルカ集 Op.6 に含まれるものより更に前の作曲と思われるものも含まれており, 彼の晩年の作品に見られる深い表情の雛が現れる前の 「わかりやすい」様式の小品たちだが, これらがマズルカというショパンのポーランドへの想いの込められた若い頃の作品で, しかも彼の死後に残されたものであることを知って弾いていると, 遠い過去の幸福を懐かしむような,喜ばしいような悲しいような不思議なノスタルジーに包まれてくる. 特に Op.59, Op.63 と,傑作だが持って行き場所のないような重苦しさを持つマズルカたちを作品番号順に弾いた後に, これらの遺作が来ると,その不思議な死んだ後の世界のような浮遊感はなおさらである.
杉浦日向子の『合葬』では,上野戦争で若者がどんどん惨死してゆく.たまたま戦争にまきこまれてしまって, もともとはこの戦いに参加していたわけでなかった, 長崎でフルベキの弟子になるはずだった若者の死もそうした無駄死にの一つとして描かれているのだが, 最後に置かれた後奏のような掌編では,この若者が死なずに長崎に留学している, という,あったかもしれない小春日和の温もりのような,想像上の過去からの未来の話が描かれている. ショパンのマズルカ集の最後に置かれているこれらの遺作の作品を弾いていると, しきりと,この杉浦日向子さんの,ありえなかった長崎留学のエピソードが頭をよぎるのである.
ゴールデンウイークに Rem Urasin のマズルカ集の CD を買った. これは前から YouTube で聞いて気になっていた CD で,特に彼の設定しているテンポが僕のテンポに近いので, このテンポで彼が何をしているのかをきちんとチェックしてみたいとずっと思っていたのだった. この CD では作品が (想定される) 作曲年代順に並べられているので,生前の作品番号のある作品の間に Opus Posthumus のフォンタナの編集の曲や,その他の比較的新しく発見された, ドビュッシー版のマズルカ集には含まれていないものなどが, 置かれることになる.Tatiana Shebanova には作品番号順の (したがって作品番号のある作品のみの) ショパン全曲集があるので (この CD 集は,何年か前の僕の誕生日学会に参加してくれた Aleksander Błaszczyk 先生に,その折に誕生日プレゼントとしてもらって以来愛聴しているが,彼女の弾いたマズルカは, 楽譜から僕に聞こえてくるマズルカとはかなり違う) これに対抗したのかもしれない.
作品の様式から,配列順序はほぼ妥当に思えるのだが,上で書いた,Op.68, No.4 は CD の最後に置かれていて, フォンタナらの演出した「死の直前に書いたもの」という神話は踏襲されている.一方, Urasin の弾いているのはフォンタナ編集のものではなく, 多分比較的最近に出版された復元版で (最近と言っても何十年か前のものらしく, 多分同じ復元版を弾いているミケランジェリの演奏もある), ABACA 形式のものである.Op.68, No.4 には,一ページからなる手稿が残っていて,この手稿の pdf はインターネットからダウンロードすることができる.編曲されたものの C の部分はフォンタナ版には全く含まれていなくて ABA で終っている (フォンタナ版はショパンの死の直後に出版された Franchomme 版とほぼ同じもののようである.), 手稿でここの部分に対応するのは, ベージの左下1/4くらいを占める部分に, 沢山の書き途中のものが線で消されて10小節分くらいが残っているなぐり書きの断片である. この編曲というか補筆では, A は2回目に左手の和声に変奏が多少加えられるが,右手は毎回全く同じで,ショパン,特に後期のショパンが ABACA 形式で曲を書くときに,2回目や3回目の A に加えることのある,あっというようなひねりを知っていると, ひどく間がぬけて聞こえる.
同じ編曲でも, フォンタナの編集したショパンの遺作のワルツでは,このショパネスクなひねりが加えられているものがあって, これを嫌う人もあり, 特にフォンタナが (ショパンがフランス系の人だったように) イタリア系の人だったため, ポーランドの国粋主義的文化人から目の敵にされるところがあるようである. しかし,フォンタナの編曲はショパンの音楽の気品を損っていないように思えるし, 僕が弾くのもオリジナルではなくフォンタナの編曲の方である.
この最後の Mazurka に戻ると, フォンタナ版の方はトルソとしての気品があるのに,この補筆版の方は, ショパンの幻の作品と偽って出版されたことのある Charles Mayer のマズルカ (Charles Mayer 自身が詐欺行為をしたのではなく, 彼の死後に彼の忘れられた作品を誰かがショパンの作と偽って再出版したか, 手稿をショパンのものと偽って高く売ったかなにかしたもの) と同格くらいの駄作のように思えてくる. Urasin が DC のために,この新しい編曲を選んでいるのを知ったことで,僕の彼に対する評価はいっぺんに下ってしまった.
Op.68, No.4 は作品番号があるので,Tatiana Shebanova も全集で弾いているが, 弾いているのはフォンタナ版の ABA である.彼女は,帰ってきた A のところでフレーズの終りごとにだんだん長くなるフェルマータを入れて,ためらうような, (死の世界に帰ってゆくような?) 演出をしているが, これもちょっとやりすぎのように思える.
一つ前の記事でも書いたように, この表明は,数理論理学の正しい知識を持っている人が見たときには,ナンセンスとしか言いようがないのだが, そのような表明が,現在でも絶版にならず (つまり版木を割ることなしに) 流通している出版物に書かれている,ということは, そのナンセンスさや「痛さ」を理解できるためには,平均以上の知性や予備知識が必要となる, ということなのかもしれない.つまり,そうだとすると,この「平均」がおそろしく低いということだろう.
しかしそう言っているだけでは何も始まらないので,この「おそろしく低い平均」を上回る事項の説明をここで試みてみたい.
そもそも,この表明の意図された内容とそのおかしさが理解できるためには, ここで暗に言及されている,また, この表明の書かれている本でも (不正確さを伴って) 説明されているところの, 数学や数学史上のいくつかの事柄を理解する必要がある.
まず 「たとえ矛盾まみれであっても」というのは, 20世紀の初頭に発見された集合論の逆理 (パラドックス) に関する話を念頭に置いているものであろう. 集合論の逆理としては, ラッセルの逆理, カントルの逆理, ヒルベルトの逆理 などが知られている. これらの逆理は, どれも,ある性質を持った集合の全体からなる集合が存在すると仮定すると, そこから矛盾が導かれる,ということを示しているに過ぎず, 「ある数学的対象を集めた領域 (たとえば群の全体, 線型空間の全体など) を考察することができる」ということと 「ある数学的対象を集めたもの (たとえば $\mathbb{R}$ 上の関数全体, $\mathbb{R}$ のボレル部分集合の全体など) を集合として (つまり他の集合の要素となりうる対象として) 考察することができる」 ということの差を認める限り, 逆理などではなく,単に,そこで述べているような性質を持つ集合の非存在定理に過ぎない. カントル自身は,この 「ある数学的対象を集めた領域を考察することができる」ということと 「ある数学的対象を集めたものを集合として考察することができる」ことの差異を正しく理解していて, 1899年前後に書かれたヒルベルトやデデキントへの手紙では, この二つの区別をツェルメロの1908年の論文でのものと類似の 公理系 を用いて説明している. カントルの公理系は発表されることなく, 次の世代の数学者たちによる, その後の集合論の発展には寄与しなかったというのが一般的な見方であるが, Akihiro Kanamori はツェルメロ全集の解説の中で, ヒルベルトはこの手紙の内容をツェルメロに話していた可能性もある,と述べている.
この二つの区別が認めらず,これを数学の重大な危機と認識したのは, カントル,ヒルベルト, ツェルメロらではなく,むしろ集合論と論理を同一視する哲学的立場で数学の基礎づけを研究したフレーゲであった. また,フレーゲとは立場が異なり互いに批判的な評価を下してもいるデデキントも, 彼が「数の理論を扱かう論理学の部分の基礎付け」(Dedekind, "Was sind und was sollen die Zahlen", 1888) というときの「論理学」が今の言葉で述べたときの 「素朴集合論」に相当するものであったと解釈せざるを得ないことを思い出すと, 20世紀の初頭に,晩年のデデキントがこの状況を 「数学の重大な危機」と認識したであろうことは想像に難しくない. デデキントは「普通の」数学者のコミュニティーに属しているとみなされていた人なので, 彼の認識が「普通の」数学者たちに伝染して,それが,巡り巡ってこの「矛盾まみれ」の人の発言に連なっている, ということも考えられるかもしれない. しかし,デデキントもあるかもしれないが, 実際には,ロジックや集合論の研究に関与していたその他多数の人たちの中にも, 一般受けするために,この 「数学の重大な危機」をよく考えずに安売りしまくった人が (過去にも最近にも) 沢山いて, そういう人たちの一般向け解説が伝染して,この「矛盾まみれ」発言が出てきた, というのが実際のところではないのかとも思える.これは,現代, ロジックのコミュニティーがコンピュータテクノロジーへのロジックの応用を無闇に強調して生き残ろうとしたり, 「純粋」数学者が数学の応用を安易に強調して生き残ろうとして,際限なく劣化していっているのと, 似たり寄ったりの現象,と言えるかもしれない.
一方,「楽園」というのは,ヒルベルトの 1925年に書かれた „Über das Unendliche“ (無限について) という論文に出てくる
„Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können.“
(「カントルの創造された楽園から何人も我々を追放したりすることはできない.」)
という有名な言葉に因む.もちろんこれは聖書の genesis への言及で schaffen (創造) するのは神なので敬語を使って訳してみている (実際には,神は絶対なので, 日本語の敬語で語りかけることすら不敬なのかもしれないが). ヒルベルトがアッカーマンとの共著で „Grundzüge der theoretischen Logik“ を出版したのが 1928年で, この本のもとになった講義が行われたのは 1917年から1922年である. アッカーマンの数論の体系の無矛盾性に関する学位論文も 1925年なので, この時点ではヒルベルトのプログラムの遂行は着実に進展していて, 上の論文を含むいくつかの場所での発言を総合すると, ヒルベルト自身は,このころプログラムが成就するのは時間の問題だと考えていたのではないかと思われる. したがって,この論文の中では 「数学の危機」が言及されているとしても, 「楽園」云々の言明でヒルベルトが集合論を擁護しようとしているのは, 集合論が無矛するかもしれないという危惧に対してではない.ここでヒルベルトが 「我々」を楽園から追放するための策略をめぐらせている蛇として想定しているのは, むしろ,強く制限された構成的な数学しか認めようとしない人たちや 「直観主義」を提唱する人たちである. この事情はヒルベルトの上記の1925年の論文全体を読んでみると明快に理解できる. たとえば,ヒルベルトが1930年のラジオ放送でも使っている "敵性"用語である „Ignorabimus“ (不可知性) は,この論文でもラジオ講演でと同じように全否定的に言及されている.
完全性定理も不完全性定理もそれらが証明されるまでまだ数年を待たなくてはならない時点で書かれている, この „Über das Unendliche“ は,現在の視点から,現在の時点での数理論理学の知識を多少は持っているが ここで述べたような歴史についての予備知識を持たない読者が読むとすると, 私が問題にしている「ここでヒルベルトが, たとえ矛盾まみれであっても, 集合論という 「楽園」の存在を固く信じていたことが思い起こされる」 という文言の出てくる本での数学の基礎づけに関する記述と同じくらい, あるいは,ひょっとするとそれ以上おかしなものになっているように見えるだろうと思う. こういったところにも, 現在の時点での数理論理学の勉強をしたことがなくて, それに至る数理論理学の発展の紆余曲折の経緯についても知らない数学者が, 高名な数学者の論文を斜め読みして数学の基礎づけについて論ようとするときの落とし穴がひそんでいるように思える. 例えば, ガロア理論を論じるときにガロアの言葉遣いを踏襲して論じるということは数学史の専門的な議論ででもない限りありえないだろう. しかも仮にガロア理論を論じようとする人は, 普通だったら, 現在のガロア理論の定式化を全く知らずにそれをするとおかしなことになるということに気がつくだろう. 一方,20世紀の前半にほとんどゼロから出発して大きな発展を遂げた数理論理学では, たとえばヒルベルトの1920年代の論文をそこでの言葉どうりに取ることは, 現代においてガロアの言葉遣いを踏襲してガロア理論を論じる, あるいはライプニッツの言葉遣いを踏襲して解析学を語ること以上の錯誤があると思ってよい. むしろ,パスカルの言葉遣いを踏襲して (現代の) 解析学を語る,くらいの錯誤がある, と言ってしまってもいいかもしれない.
このヒルベルトの論文は,最後まで読んでみると, Gödel による $V=L$ で一般連続体仮説が成り立つという 1940年代の結果の証明の雛形になっているのではないかとも思われる, 連続体仮説の肯定的証明の (論文の中でヒルベルトの計画が成就したときには証明として完成することになると宣言されているところの) 証明のスケッチが与えられている.このヒルベルトの「証明」は謎だが, ヒルベルトはヒルベルトの計画が実現したときには,数学の完全性から, 現在の数理哲学の用語を用いて言うと predicativity と impredicativity の間の差も解消する,と思っていたのではないだろうか.
数学の無矛盾性を純粋に確定的な立場から (aus dem finiten Standpunkt) 証明することを目標とするヒルベルトのプログラムは, ゲーデルの第2不完全性定理により, その不可能性が証明されたし, 数学 (=集合論) の完全な公理系を確立することの不可能性が第1不完全性定理で示されたことにより, predicative と impredicative の間の溝も,少なくとも simple-mided な形では,永遠に埋まらないことがはっきりしたわけだが, そのことと「矛盾まみれ」という感覚の間には大きなギャップがある. 「純粋に確定的な立場からの無矛盾性証明が存在しない」ということは, 矛盾が存在することを言っているわけでは全くないし, 矛盾がみつかっているわけでもない.むしろ,直接的な証明ではありえないとしても, 数学が無矛盾であることの, 数学の範囲ごとの様々な度合の無矛盾性の間接証拠や (純粋には確定的でない立場からの) 証明が見出されている. この意味で 「矛盾まみれ」というのはどう考えても異様で, 何を言っているのかが全く分らずに発言されたのでなければ, これは,この表明をした人の思考の混乱を記述しているにすぎないのではないか,と思われる.
ゲーデルの不完全性定理がヒルベルトの計画を (完全にではないにしても) 挫折させることになったことを考えると, ヒルベルトがゲーデルの $V=L$ の結果を予言するような表明を,ヒルベルトの計画を擁護する, ほとんど政治的プロパガンダのように見えるこの論文に書いていることは 歴史の皮肉とでも言えるように思える. 実際ヒルベルトは, この論文を書いたときに,„ignorabimus“ を肯定する人たちを何としても打倒しなくてはならない, という強迫観念にかられていたのではないだろうか --- そう考えると, その想定されるバイアスのもとでは, このときから少し後の, 彼の息子との確執やアッカーマンとの確執も, ヒルベルトの個人史の中のエピソードとして, 一つの文脈の中ので考えることができるようになるように思える. ただし 「ここでヒルベルトが, たとえ矛盾まみれであっても,...」の著者は, 少なくとも数年前に本人と話をしたときには $V=L$ についてさえ全く何も知らなかったので, この 「ここでヒルベルトが,たとえ矛盾まみれであっても, ...」という表明には, ここで述べたような歴史の背景に対する揶揄は含まれていようはないし, 彼には,ヒルベルトの息子との確執やアッカーマンとの確執についても, それらのエピソードを知っていたとしても, 上で言ったような背景のもとでの逸話としては見ることができなかっただろう.
「ここでヒルベルトが, たとえ矛盾まみれであっても, 集合論という 「楽園」の存在を固く信じていたことが思い起こされる」 という表明が, 痛い,あるいはこの場合むしろ薄気味悪い,ものになっている,もう一つの理由は, この表明が,この著者の書いたものの中で,「たとえ矛盾まみれであっても,旧来の数学という 「楽園」の存在を我々が固く信じていることが思い起こされる」 という思考には全く結びついていないことである.実は, 矛盾まみれの数学 でも書いたように, 現代の数理論理学は,「集合論は矛盾まみれと言うことができるとしても, 通常の数学はそうではない」という主張の論拠とできるような結果を複数持っている. しかしこの著者は,そのような議論に踏み込むことは全くない.これは, 知らないので踏み込みようがない, というだけなのかもしれないが,この本では, 自分の旧来の数学に対する盲信が (そのことの妥当性は如何については別としても) 盲信でしかない, かもしれないことを理解していること,を示唆する表明すらない.
独裁政権や他国に支配されていた国が“解放”されたとき, 解放前に,どうしようもない opportunists だったり, 占領国の collaborators だったりした人たちが,新体制の上層部や官僚として沢山生き残って, この人たちが旧体制を demonstrative に,しかし何かしらやぶにらみな議論で批判する, という現象が普遍的に起る. これはヨーロッパでも日本でも日本の近隣国でもごく最近にも広く起った/起っていることである. 数学は集合論から「解放」されたわけではないのだが,この著者は, 「カテゴリー理論こそが集合論に代る新しい数学の基礎 (づけ) である」 というようなプロパガンダに踊らされて,解放の幻想を抱いている可能性があるので, 比較検討してみる価値もあるかもしれない.ちなみにカテゴリー理論は,ZFC では, ZFC の超数学に含まれている,と考えることのできるものである. 現代的な集合論は,相対的無矛盾性の研究などを含め,ZFC の体系内の数学と, ZFC を外から見て議論する超数学の間を頻繁に行き来する, という旧来の数学にはほとんど現れない議論が展開される.このことは, 旧来の数学を研究している人々には全く見えていないことなのかもしれないので, この「カテゴリー理論こそ ...」という,もっと痛い思い込みも, その意味では仕方がないことなのかもしれないとは言える.しかし, こう書くと被害妄想的な発言ととらえられるかもしれないが, この 「カテゴリー理論こそ ...」という盲信は集合論の研究者の迫害の一つの論拠になっているように思えるので, (迫害ということで言えば,たとえば私は,日本では,ついに数学科のポジションを offer されることはなかった) 「仕方がないことなのかもしれない」と言って放置していい状況ではないようにも思える. [このパラグラフはまだ書き途中です 19.07.27(土12:45(JST))]
ゲーデルによる完全性定理と不完全性定理により, ヒルベルトの計画の基礎としてヒルベルトが導入した証明の体系は (ある意味で --- つまり証明に現れる論理式のモデルでの解釈という考え方を認めるなら) 完全であることが証明され, 一方,ヒルベルトの計画の方は, ヒルベルトが思い描いていたようには成就しえないということがゲーデルの不完全性定理から分かったわけだが, 同じ不完全性定理のバリエーションであるゲーデルの加速定理が, 構成的な数学のみを許容する立場からの批判から集合論を強く擁護することは, 見逃されていることが多いように思える.
筆者は,最近 [1] 渕野昌, 数学と集合論 --- ゲーデルの加速定理の視点からの考察, 科学基礎論研究,Vol.46, No.1 (2018), 33--47. でこのことについて議論した. たとえばヘルマン・ヴァイルの 『連続体』に書かれているような構成的な数学の視点からの数学の基礎づけについての議論は, 不完全性定理以降の数理論理学から見ると,数学の基礎づけとしてはある意味で全く obsolete になったとも言えるし, それが逆数学で扱われる体系の一つに対応しているという解釈で現代に蘇ったと言うこともできる (このことについては, [2] 田中尚夫, 渕野昌 訳/解説,ヘルマン・ヴァイル著,連続体 ,日本評論社,(2016). の本文の脚注を参照されたい.). この逆数学での体系は集合論に比べるとはるかに無矛盾性の強さの小さい (つまりごく平たくいうと無矛盾である確率が高い) ものになっているので, そこから見たときには,集合論を「矛盾まみれ」と形容することはできるかもしれない. しかし,私が [1] でも説明したように,その視点から見たとしても, (集合論での) 数学研究は無視できないものになっているのである.子細は [1] に委ねるが, 要点は,ある十分に強い公理系 $T$ を真に拡張する公理系 $T'$ では,$T$ での証明より $T'$ での証明の方が格段に短かくなるような $T$ の定理が存在が証明でき (Eurenfeucht-Mycielski の加速定理), $T'$ が $T$ の無矛盾性を証明する場合には,証明の短かさのより詳細な指定の下で, そのような $T$ の定理が具体的に構成できる (Gödel の加速定理) ということである. このとことは, 通常の数学が必要としている公理的枠組をはるかに越えた集合論で議論をすることの (プラグマティックな) 有用性 (の可能性) を結論するし, 通常の集合論の公理系の無矛盾性を楽々と証明してしまう, 巨大基数公理を集合論に付け加えた体系で集合論を研究することの,意義の強い根拠ともなっている.
これらの定理は,ある数学的命題について,集合論の公理をフルに使ったときには, その短い証明が簡単に見つかるが,旧来の数学が十分に展開できる程度の部分体系では, 同じ命題の証明は非常に長い複雑なものにならざるを得ない,更には, 可能な最小の長さが大きすぎて物理的に書き出すことができない, という状況がいつでも生じる可能性があることを示しているからである.
このような意味で,集合論と旧来の数学の間の関係は,「ここでヒルベルトが, たとえ矛盾まみれであっても, 集合論という 「楽園」の存在を固く信じていたことが思い起こされる」 と他人事のように言うことが適当な状況には, まったくなっていない,と言えるはずなのである.
数学者は論理的な推論から自分の直感と異なる結論が導けてしまう, という体験をたくさん積んでいるはずなのだが, 自分の専門分野では, そのような体験を段階的に積みながら自分の数学的直感の方も少しずつ修正していっているので, 逆にプロの数学者は,それを体系の矛盾と混同してしまうような,自己の 「数学的直感」と数学の間の乖離を経験することがほとんどなくなってしまっているのかもしれない.
それで,数理論理学や集合論をどこでも勉強したことのない数学者が, 彼らの言うところの 「数学基礎論」に関連する話題で, 自分の分野では感じることの少なくなっている大きな直感からの乖離に直面して, それを,論理学や集合論の体系が矛盾している,と誤認してしまうことが多いのだろう.
これを書き出したのは, ある知りあいの数学者による数学の哲学や数学の美学のようなことに関する本の中に, 「... ここでヒルベルトが, たとえ矛盾まみれであっても, 集合論という「楽園」の存在を固く信じていたことが思い起こされる」 という一節があったのを思い出したからだった.数年前にこの本を読みなおしてみて, この「矛盾まみれ」をはじめとして,あまりにも痛すぎるところがいくつもあったので, 売れていそうな本なので次の版が出る機会に訂正ができるかもしれないし,助け舟を出してあげようと思って, 会ってこの本についての話をすることを著者に提案してみたことがあったのだが, 忙しいという理由で見事に断られてしまった.
面白いのは,この人もそうなのだが,集合論が矛盾まみれ, という感覚が (仮にそれが正しい直観だとしても) , 「そうだとすると,自分のやっている「数学」も実は矛盾まみれである」, という結論に全く結びつかないように見えるところである.もちろん, logic を知っていれば,たとえば,consistency strength の hierarchy による議論などで,自分のやっている数学は集合論の非常に弱い部分体系の中で展開できるから大丈夫だ, などのある妥当な理由をつけることはできるとは思うが, たとえば,この本では, 読んでみたかぎり,著者御本人がそのような議論を理解しているようにも思えないのだ (本人と話したときの感蝕としては,この著者は Peano arithmetic が何かも知らないようなので,この consistency strength の hierarchy 云々を理解するために必要となる予備知識を初めから全く持っていいないと断言できるかもしれない). また,この本には不完全性定理についての話も出てくるのだが, 不完全性定理が自分のやっている数学とどう関わりあっているのかについても, この本では,はっきりと言及されていないので,疑ってかかると, その点についても,ちゃんとつきつめて考えたり理解しているのかどうかも怪しいような気がしてくる.
今 (2019年前期),大学院の講義で,集合論の公理系の導入のところの話をしている. まず,素朴(公理的)集合論を導入して,そのうえで述語論理を (純粋に finitary な standpoint にもどって) 導入し,(ラフな) コーディングの話を経由して, 完全性定理の略証を与えておき,そこで初めて述語論理上の集合論の公理系の再導入をする, という筋書を考えている.更に,この段階で,コーディングの $V_\omega$ でのもっと厳密な再導入をして, 不完全性定理の話を集合論の枠組で行なうことになると思う. これは歴史的な発展にも近い形だが,正しい理解を与えるための筋道としては, この少し回りくどいやり方をする必要があるのではないかと思う.
このような導入の過程で,集合論が旧来の数学をどのように内包しているのか, 集合論のどの subtheory がどれだけの数学を包含するものになっているのか, といったことの説明のプレゼンテーションをどのようにつけることができるかを確かめる, というのが,この講義で実験してみたいことの一つである.この実験の成果は, 最終的には, なかなか書き上がらないでいる集合論の教科書 (複数の本になりそうである) に盛り込まれるはずである. そしてそれは,旧来の数学を研究している数学者にも読んで理解してもらえるものにしたい, とも思っている. しかし,これは,上で述べたような経験や数多くの似たような体験を思い出すと, なかなか難しいことかもしれない.... と考えると,かなり絶望的な気分になってくる.
僕は1979年にドイツに留学して本格的な数理論理学の勉強を始めたのだが,その直前に, 早稲田大学で,この Red Book の最後の部分の証明の細部についてセミナーで話をした. 記憶に間違えがなければ,このとき高田正之君や高橋真君もこのセミナートークの聴衆の中にいたと思う. 適当な指導者がいれば, 何か別のものを読んでいたと思うが,このころはほとんど独学に近い状態だったので, これはいたしかたなかった.しかし, この本を読みこなせた,という事実自身は, その後ベルリンで勉強を続けるときの心のかてにはなっていたのではないかと思う.
"Green Book" の方は, 新版の "Millennium Book" (Set Theory -- The Third Millennium Edition) には含まれていないトピックスが沢山入っているので, 今でも必要になることのある本である.僕はといえば, この本は,大昔に (多分ベルリンの,当時 Heidelbergerplatz にあった Springer 直轄の数学書書店で) 買ったものをスキャンして ipad に入れて携帯している ("Millennium Book" の方は, それほど大昔ではないがもう十年以上前に著者自身から貰った pdf をこれも ipad に入れている).



この映画の中のシーンの一つは,今回のアメリカ出張の後半に立ち寄った Raleigh が舞台だった. そんなこともあってか,その週末に訪れた Raleigh の歴史博物館 には, この Green Book の期間限定の特別展示があった.


Autism の人たちは Bach を好む.Bach の音楽には完璧な構造があって,彼等はそこに安らぎを見出すからだ.
昨年の秋にもポーランドに長期間滞在していたのだが, 滞在の終りが近づくにつれて土地の言葉がしゃべれない状況にだんだんうんざりしだしていた. ENGLISH AS A SECOND LANGUAGE: WHO IN EUROPE SPEAKS IT BEST? というリストで見ると, ポーランドは, 第2言語として英語をよく話すヨーローッパの国のランキングで9位に入っていて, 例えばフランスやスペインはこのリストに入ってもいないのだが, これは多分「教育を受けた」人たちについてで,たとえば workmen のおじさんたちが英語ができるかと言えばそうではなくて, そういう人たちとジェスチャーをまじえて意思疎通をする,という冒険 (実際, 去年のポーランド滞在では,停電とか水廻りの故障をはじめとして,けっこうの回数トラブルが発生したので, それに対応するために言葉のほとんど通じない相手とのコミュニケーションをとる必要にせまられることが何回もあった) は楽しくもあるが, いささかフラストレーションがたまることでもあった.それから, 子供たちと言葉で交流ができない,というのも,とても残念に思えた.
その点,イギリスは英語の本場なので,英語がどこでも通じて,非常に気が楽だった. もっともイギリスは,それが Brexit の一つの背景になったことでも知れるように, ポーランド人の労働者がやたらに多くて,ホテルの cleaning personals のおばさんやおねいさんはほとんど全員ポーランド人なのだが, ポーランドでの同様の職業の人たちとは違い,彼らはそこそこ英語ができる.
僕の英語だって,日本語やドイツ語ほどには流暢でないし (といっても,僕の日本語やドイツ語だって, 少なくとも口語に関してはあまり流暢と言えるものではないかもしれないが…), 僕の生成する英語の文章はかなり artificial なものでもあるはずなのだが, 英国人が紳士的だからなのかもしれないが, 必要なときには街で普通に普通の人と会話が成立したり, タクシーの運転手さんと普通に雑談ができたりするのはちょっと不思議な, しかしとても楽しい経験だった.
神戸とブリストルの共通点は何だろうかと考えてみた, 両方の街とも, かつて重要な港として栄えた場所だということがあるだろうが --- もちろん,それとも連動しているのだが --- 両方とも吊り橋 (suspension bridges) のある街である,という答もありえるのではないだろうか.それで, 僕の talk の スライド は, これらの橋の写真でしめくくってみた.3つある橋の写真のうち最初のものはもちろん明石大橋で, 3番目のものが,ブリストルの Clifton Bridge である.その間にはさんだ橋の写真は, 去年のポーランド滞在でも二週間ほと住んだ Wrocław の,大学の数学研究所の向かいにある Grunwald bridge (Most Grunwaldzki) である.
ここで御本人の発言として書いてあることは, 二宮さんの解釈が多分に混じっているかもしれなくて,それを更に僕の言葉で要約すると, 本人のもとの発言とはかけはなれたものになってしまう危険もあるのだが, あえて書き出してみると,曰く, 「岡潔先生は,数学とは情緒を数学という形式で表現する学問である,と言ったが, 1930年代以降の数学は情緒のないように作られていて面白くない」 「ヨーロッパの数学者(の大半?)は(第二次大戦前後に)アメリカに渡って (彼らの数学は?) アメリカナイズされてしまった」 「今の数学は問題は解けるが問題は作れない」等々.なお,この1930年以降というのは, 数学の "メインストリーム" が logic での研究を理解できなくなってきた時期とも重なる. また「抽象的…」というような発言もある.
この記事では,「本当の数学って何なんですか」という質問に対して,僕が 「その人が数学と思ってやっていることが,数学でしょう」と言ったことになっている. 確かにそのような発言をしたかもしれないが,しかし,そうだとすれば, それは, 「真の数学的創造性が発揮されているのであれば」というような暗黙の前提で言っていたことで, 過去の数学をいつくしむ, ことと,数学的創造性の発露を同等に並べて言っているわけではない. もちろん過去の数学の枠組から出ずに創造的な数学を行なうことも不可能ではないだろう.
例えば,Federico Mompou (1893--1987) は,過去の音楽の語法からほとんど踏み出すことなく, それでいてどこにもない, ちょっとでも手でさわると壊れてしまうような精妙な新しい響きの音楽を作っていて, そこには,"映画音楽もどき" の作曲をする人たちの音楽とは全く異なる純粋な音楽的創造性の発露が見られるのだが, 似たようなことが数学でも不可能ではないかもしれない.しかし, どうも高瀬さんの言っていることは,そのような数学の創造ではないようである.
Claude Debussy (1862--1918) は,彼のオペラがメロディーを抹殺した, という批評に答えて,そんなことはない自分の音楽はメロディーに満ちている,と答えたということだが, 僕も,もし僕の数学には情緒がない, と高瀬さんが批判しているのだとすれば,そんなことはない僕の数学は情緒に満ち満ちている,と答えるだろう.
Since the following theorem is about the non-existence of a proof in meta-mathematics, it is a kind of a meta-(meta-mathematical) theorem.
I would like to thank Taishi Kurahashi and Makoto Kikuchi for some valuable comments.
Theorem.
Assume that $T$ is a weak set theory in a broad sense
(including, e.g., the case “$T={\sf PA}$”) in which the Second Incompleteness Theorem can be
formulated and proved. Let $T'$ be a theory
extending $T$ and
such that $T'\vdash consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})$.
If there is a (meta-mathematical) proof of the consistency of $T'$ from the assumption
that $T$ is consistent, then we can obtain a proof of the contradiction from $T$.
In other words, there is no (meta-mathematical) proof of the consistency of $T'$ from the assumption
that $T$ is consistent.
Proof. Assume that there would be
$(1)\ \ $ a (meta-mathematical) proof of the consistency of $T'$ from the assumption that $T$ is consistent.
Then we should be able to translate this proof to a proof of $consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}^{\urcorner\urcorner}) \rightarrow consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T'}{}^{\urcorner\urcorner})$ from $T$. Thus, we have
$(2)\ \ $ $T\vdash\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T'}{}^{\urcorner\urcorner}) \rightarrow consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T'}{}^{\urcorner\urcorner})$.
Note that, since our meta-mathematics should be strictly constructive, the proof $(1)$ must give
$(3)\ \ $ an algorithm $\cal A$ such that, given a proof $\cal P$ of the contradiction from $T'$, $\cal A$ gives us a proof ${\cal A}({\cal P})$ of the contradiction from $T$.
By the Deduction Theorem of a standard system of first-order logic, in which we formulate the formal proof for $(2)$, it follows that
$(4)\ \ $ $T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})\vdash \ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T'}{}^{\urcorner\urcorner})$.
By the assumption on $T'$ it follows that
$(5)\ \ $ $T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner}) \vdash\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})\ }{}^{\urcorner\urcorner})$.
By the Second Incompleteness Theorem (applied to the theory $T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})$), it follows that $T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})$ is inconsistent. Since $T\ +\ consis({}^{\ulcorner\ulcorner}\hspace{-0.1ex}{T}{}^{\urcorner\urcorner})$ is a sub-theory of $T'$, $T'$ is also inconsistent. Hence, by the algorithm $\cal A$ in $(3)$, we obtain a proof of the contradiction from $T$. Q.E.D.
The theorem above applies to many situations in set-theory. For example:
There is no meta-mathematical proof of the consistency of $\sf ZFC$ $+$ “there is an inaccessible cardinal” from the assumption of the consistency of $\sf ZFC$ (provided that $\sf ZFC$ is consistent);
There is no meta-mathematical proof of the consistency of $\sf ZFC$ $+$ “there is a measurable cardinal” from the assumption of the consistency of $\sf ZFC$ or even of the consistency of $\sf ZFC$ $+$ “there is an inaccessible cardinal” (provided that the theory $\sf ZFC$ or $\sf ZFC$ $+$ “there is an inaccessible cardinal” respectively is consistent), etc.
Wrocław では,大学の音楽ホール Oratorium Marianum のピアノを弾かせてもらうことになり,何回かこのホールのピアノで練習をした. Katowice の Aula にあるのと同じ銘柄の Seiler のピアノだが, こちらに置いてあるのは,モダンな多分戦後の楽器で, あまり特徴もないし,弾きやすくもない楽器だった. しかし,ホール自体は興味深いものだった. パガニーニやリストやクララヴィクだった時代のクララシューマンも演奏会を開いたことがあるというホールは, reconstruction ではあるが,装飾過多のバロック様式で, 客席に人がいないと残響がひどく長くて,弾いていると昔の銭湯で歌をうたっているようないい気分にはなるが, 後にひっぱられて早いテンポでは弾けなくなってしまう.この状態でプローベをした後で, お客が入ってから本番の演奏をすると,テンポを保持するのがすごく難しくなるのではないかと思う.
日本がアメリカに占領されていた時代には, 日本での台風の正式名はアメリカ式にアメリカ女性の名前だったので, キャサリン台風や, ジェーン台風やキティ台風など,歴史に残る台風があって,その名前を聞いただけで1940年代後半から1950年代にかけての, 空襲で広くなった戦後の空が思い出される.自分の生れていなかったころの記憶というのは, 不思議なものだが,その時代のことを書いたものや, かつて聞いたその時代を知っていた人の話, その時代を描いた映画などの記憶や子供の頃の記憶の過去への敷延から, 自分が経験したことのような鮮明な (作られた) 記憶が浮び上がってくる. 僕の言語生活では, ドイツ語の割合が高いのだが (少なくとも読み言葉や聞き言葉 (テレビやラジオでの) の passiv な受容に関しては日本語や英語よりずっと高いと言えると思う), 僕がドイツ語を使うようになる前のドイツ, たとえば 1940年代から1960年代にかけての (西)ベルリンなども, 鮮明な,偽の (しかし,十分に史実と kompatibel な) 記憶があって, その時代の臭いをかぐことができる. それで,Ku'damm 56 なんていうテレビ映画を見たりすると, あの時代のベルリンへのなつかしさ (... die Seligkeiten vergengener Zeiten ...) がこみあげてくる.
キャサリン台風といえば, この名前を冠した西脇順三郎の詩 『キャサリン』がある. この女性の名前からくるエロティックな連想をつつみこんだ詩で, 「女から/生垣へ/投げられた抛物線は/美しい人間の孤独へ憧れる人間の/生命線である」 に始まって,「この手紙はもうあなたへは出さない。」で終っている. もちろん台風との関連は詩の中では隠されている.詩の作られた時期を考えると, 台風の名前との関連は自然に思えるが,この関連を確定的に言いきるには, 詩人を知っていた人の書いたものなどを読む必要がある. 西脇順三郎には『秋 II』という, 『キャサリン』と同じ詩集に収録された,台風が explizit に出てくる詩もある.
秋
II
タイフーンの吹いている朝
近所の店へ行つて
あの黄色い外国製の鉛筆を買つた
扇のように軽い鉛筆だ
あのやわらかい木
けずつた木屑を燃やすと
バラモンのにおいがする
門をとじて思うのだ
明朝はもう秋だ
日本文化には, その出発点に,ヨーロッパ文化でのような意味での「真理」の概念が存在しないかもしれないので (*), この「区別について認識すらできない」ことはむしろ当然のことなのかもしれない.いずれにしても, そのような認識の混濁のある個人を批判しても,批判するだけ無駄と言えるかもしれないし, それでもあえて,そのような人たちを批判すると, これは動物虐待に類することになってしまいかねない.
日本語で数学の本を書くということ では, そのような 「日本語で書かれた本の読者の多く」のうちの一人の “カスタマーズレビュー” を例にとって, そこでの認識の混濁の分析をしてみたわけだが, そこで例として挙げた文章の,おかしさは, 書かれたことの意味に深く踏み込なくても,アルゴリズミックに選別することが可能だろう.
しかし, 一見まともな人が書いたように見える文章だが, 実はもう少し高次の問題点を持っているという種類の “カスタマーレビュー” というのも沢山あって, こちらの方はもっとやっかいである. 正常の読書人として日常生活を行なうことのできる知性の最低線と, 数学を理解できるための能力の最低線の間にまだ大きな差がある, ということなのかもしれないが,次に挙げるいくつか例では, やはり,「理解する」ということについての理解の深さが問題となっているようにも思える. ただし, これはわざと悪意を持ってこのようなものを書いているという可能性も捨てきれないので, そうだとすると問題はもっと不可解でしかも不快なものかもしれないのだが.
たとえば,日本語で数学の本を書くということ でもちょっと触れた, 数学者の肩書きを持った人の書いた,破綻した内容の本に関する amazon のカスタマーレビューのひとつとして, これを書いている時点 (18.07.04(水08:33(JST))) で以下のような文章が載っている:
ゲーデルに興味をもった初学者にこの本をオススメします。
何よりよいのは、会話体の文章がとても読みやすいことです。
こういうタイプの無限論の解説書は、ギリシアの可能無限についてはともかく、
歴史を下ってきて「ラッセルパラッドクス」のあたりにくると、だんだん喩え話が
内容に追いつかなくなることが多い。その点、この本はすごく上手なサンプルを
つくることと、読者代表の理想的な聞き手を配することで、すっきり読めて、
数学的な内容も伝わってくるという理想的な記述がしているように思いました。
数学としてきちんと記述したい部分は、主となる会話体に対して囲み記事や付録に
追い出しているところもグッドです。おかげで、私の場合、コーシー列についての
理解が一段深くなったように感じています。
とても面白い本です。
これは文章だけで判断すると特に知性に問題のある人間の書いたものではなさそうに思える. しかし,ここで言っている「すごく上手なサンプルを つくることと、読者代表の理想的な聞き手を配することで、すっきり読めて、 数学的な内容も伝わってくるという理想的な記述がしているように思いました。 」というのが,この本を読んだときの感想ではありえないことは, 私が ここ で行なった分析を見れば, (少なくとも,そこで私の書いている数学的な内容が理解できるなら) 客観的な事実として認めざるを得ないだろうし, この本の著者のかかえているいくつもの大きな問題についても, (その真のありどころがどこにあるか --- つまり, 著者の能力の問題で何も分らなくてこういうことになっているだけなのか, (数学に対しての ? ) 強い悪意を持ってわざとやっているのか,悪意とまではゆかなくても, 売れる本を書くための未必の悪意が問題を起しているのか --- ということの判断ができかねないことは別とすると) 理解できるはずだと思う.もちろんここでは,「すっきり読めて、 数学的な内容も伝わってくるという理想的な記述がしているように思いました。」と言っているところの 「内容」が醜く間違っているものかどうかについては触れていないので, 「こう書いて何が悪い」という居なおりも可能なのかもしれないが.
この読者のレビューは,上で言ったように, 文章の破綻やそれを書いた人の思考の破綻をアルゴリズミックには検出できない, という程度の作文のできる能力と, 数学的な内容の破綻を感知できるだけの知力との差を例示するものになっているのだろうか ?
あるいは,このレビューアーも, やはり何かの意図をもって「わざと」このような感想を書いていて, 何か批判されたときには, 「こう書いて何が悪い」というような居なおりをするつもりでいるわけなのだろうか ?
(*) 「真理」の概念が成立するためには, 一神教的な真理の局在化が必要なのではないかと思う. こう言うと, では,偉大な数学者や哲学者たちを生んだギリシャ文化はどうなのか, という問が当然頭を擡げるが,ギリシャの神々は八百万ではなく hierarchy の中にいて,真理の局在化は一神教的ではないにしても十分に起っていたのだと思う. ただし,ここで言っているのは,背景文化としての真理であり,個人が「究極の 真理」を想定するか,想定するとするとそれをどう想定するのか,ということは, 彼/彼女の背景文化だけからストレートに出てくる結論では,もちろんないだろうが.
🚧 この項目はまだ書きかけです 🚧
特に日本語のような読める人がごく少数の言語では, 書いた文章がその文章の求めている読者にたどり着けない可能性は大きいのではないかと思う. ちなみに,手元にある少し古めの資料 [Duden, 2012] によると, native speakers の数で言えば,日本語の話者は英語の話者の三分の一強くらいもいるようで, その意味では弱小言語とは言えないかもしれないが,英語の読める intellectuals と日本語の読める intellectuals の数を比較する, ということを考えてみると,日本語が「読める人がごく少数の言語」だという主張は, 誇張でないことが納得できると思う.
幸いに僕のサイエンスカフェでの講演は英語で行ったので, スライド も当然英語で書かれている. その意味では,この弱小言語の呪詛からは自由なわけだが, スライドでは数学的な要点のみをまとめているので,この講演で口頭で述べた, これらの例を基に行った数学の一般性とその汎用性に関する議論は,これだけを見た人には全く伝わらないだろう.
この講演で扱った数学の例は初等的なグラフ理論に関することだったので, 準備のため,一松信先生の『四色問題』を読み直してみた.この本は Appel と Haken による四色問題の解決の直後に, 多分,非常に短い期間で書かれた解説書であるが (初版は昭和53年(1978年)で, 著者が Martin Gardner から四色問題が解決されたようだということを聞いたのが1976年7月のことだということである),それにもかかわらず, 問題の解決の経緯についての記述を含めて丁寧な説明がされている.
しかし amazon のこの本のページでの “カスタマーレビュー” には, 複数の “間違った読者” のおかしな感想が載っている. そのような感想の1つを引用してみると,曰く: この本を読むには、 グラフ理論とフレームワークがわかっていないと理解できない本です。一般向けの本として売られていますが、 ハードルが高くてわかりません。
『フレームワーク』が何を指しているのか不明だし, 文章が日本語としても破綻しているが, 「グラフ理論」については本書には予備知識を全く仮定しない丁寧な説明があるので, ここで書くべきなのは 「初等的なグラフ理論についての説明を分かるだけの理解力のない人には理解できない本です」だろうし, この評者は,自分の置かれている embarrassing な状況を正しく認識して,潔く 「自分にはハードルが高くてわかりませんでした」と書くべきだろう.もちろん本書は一般向けの本である.
このレビューを書いた人の知性の濁泥は, 認識の主体を文法的に特定しない日本語の構造がそれを助長しているようにも思えて非常に不愉快である. 他にもいくつかのレビューが載っているが,どれも同じくらい病的である. 気になって同じ程度の知性の読者を対象にしていると思われる英語で書かれた何冊かの啓蒙書の customer reviews を読んでみたのだが,そこでは日本語でのこれらの 「カスタマーレビュー」でのような言語や内容の乱れは見られない, ちゃんとしたレビューが大方を占めていた.英語でも,たとえばポピュラー音楽でない, ドイツ語で E-Musik と呼ばれるような種類の音楽の youtube のポストには, 一松先生の本のカスタマーレビューと十分互角に戦えるようなクレイジーな (英語での) コメントが集まってくることもあるので (関連する話題については, 「 『無限のスーパーレッスン』 の hyper-critique」の第6章に書いた) , 単に,どこで, 自分の理解を超えたものと向き合うだけの度量のない人たちが醜くストレスを発散しているか, または, ストレスを発散してもいいことになっている,と勘違いできるのか,というような状況の文化的な違いに過ぎないのかもしれないが. いずれにしても,英語で書かれた数学の啓蒙書では,それらが英語で書かれていることで, 内容について来られる読者を十分に確保できて,そのような読者の一部の書いた正統的な reviews がおかしな書込みをブロックしているが,一松先生の本は,日本語で書かれていることで, そのような ''正しい'' 読者を十分な数だけ集めることができないでいる, ということは言えるだろう. これは日本の文化の問題ということももちろんあるのだろうが, 日本語の読者の数の問題ということが大きな要因になっているのではないかと思う. 以上では,一松先生の本のレビューについての話しだが, 実は僕自身も一松先生の本のレビューに似たようなレビューをいただいたことがあるし (これについては ここに 書いたことがある.), 他の日本語で書かれた一般向けの本でも同様の現象が起こっていることが確認できる. また,後述するように「とんでも本」に「好意的な」レビューが集まるという現象さえ起こっている.
皮肉なことに一松先生の本の中にも,読み手の少ない言語としての日本語について触れているところがある. その箇所を以下に書き出してみる:
その本は、結局、リンゲル一人の名で、ヤング未亡人にささげるとして, 一九七四年にドイツの有名なスプリンガー書店の「黄表紙」叢書の一冊として, "Map Color Theorem" と題して発行された。 著者はカリフォルニアでやった仕事だから, 英語で書いたと弁解しているが,ドイツ人がドイツの書店から英語の本を出版するというのは, 政策的な感がある。他の本では、「初めドイツ語で書き出したが,good German で書くよりも,bad English で書いた方が, 広く読んでもらえると忠告されたので,英語に書き直した」といった記述さえある。 日本での外国語教育も,この面から考え直す必要があるかもしれない。
1978年に書かれている文章なので,今読むと若干時代錯誤の感もあるが, 少なくともこの時点で, ドイツでは本は英語で書くというスタンダードは既に確立されかけていて, 日本では現在でもそうでないので,当然ながら当時はそんな考えに及んでもいなかった, という状況が浮かび上がってくる.もっとも, 一松先生がここで書いているのは,数学の専門書についてで, 本書のような啓蒙書についてではないのだが.
一方,一般向けと称しておかしな内容の書いてある本に, 好意的なカスタマーズレビューが集まる,という現象も広く起ってるようである. これらのカスタマーズレビューは trolls の仕業なのか,あるいは単に間違った内容の本の香りにさそわれた知性の弱い人達なのかは不明である. もちろん出版社のさしがね,ということだってありうるだろう. それらの全てをいちいち批判しているだけの余裕はないが, 中には数学者の肩書きを持った人が書いた「驚くべき」内容の本というのもあって, これはちょっと見過すわけにはいかないような気がする.
これは多分著者だけの問題ではなくて,読者の問題でもあるのだろう,そもそも 日本語で書かれた啓蒙書の読者の多くが望んでいるのは, 真理に近づくことではなく,真理を理解したという錯覚の心地よさなのだろう.
もしや,と思ってネットを検索してみたら案の定, 「こんなに寒いので地球温暖化はおかしい」というようなことを言っている人が沢山いた. たとえば,
温暖化ってのはCO2による温室効果で起こってるんじゃなかったか 温室なんだからどこもかしこも暖かいんじゃないんかすんごい寒い…… 地球は温暖化してるんちゃうんか……(´;ω;`)
これだけ日本寒かったら地球温暖化じゃないよね(笑)
など.こういう痛い発言が当然のようにされている,
というのはやはりかなり痛いし,絶望的な気分にもさせられる.
統計の授業で,
問題. 地球温暖化が議論されていますが,ここのところ,
歴史的な最低気温の記録が更新されています.このことが
地球温暖化と全く矛盾しないことを,「平均」「偏差」というキーワードを
用いて説明してください.
というのを出したら,
どのくらいの割合の学生がまともな解答を書くのだろうか? あるいは,
物理の授業だったら,
問題. 地球温暖化が議論されていますが,ここのところ,
歴史的な最低気温の記録が更新されています.このことが
地球温暖化と全く矛盾しないことを,「平均」「偏差」というキーワードを
用いて説明してください.むしろ,最低気温がどんどん下ってゆくことが,
地球温暖化から自然に予測できる事態であることを,「温暖化の加速」,「システムの安定」という
ようなキーワードを含めて説明してください.
としたときどうだろうか?
△△△


 △△△ 地球温暖化ナリ.地球ヨサラバ.
△△△ 地球温暖化ナリ.地球ヨサラバ.
これはこれまで「地球温暖化ナリ.氷山ヨサラバ.」 としていたものだが,表現をアップデートした. まあ, 「寒いから地球温暖化じゃない」というようなことをはずかしげもなく言えるのが人類なら, 人類は滅んでも仕方がないのかもしれないという気分である. ただし,これは前にどこもかに書いたかもしれないが,どうせ昨今滅ぶのなら, 僕の時代に滅んで,滅ぶところを体験させてほしい,というのは強く思うところでもある.
京都では,たまたまホテルが安く取れたので, 一泊することにしたのだが,このホテルは京都に長く泊まる時にいつも行くピアノスタジオのすぐそばだったので, 一日目の講演が終った後で,久しぶりにこのスタジオのピアノを弾いてみることにした.
最初の一時間半はいつも借りている YAMAHA のグランドピアノだったのだが, その後の時間にこのピアノの予約がすでに入っていたので, アップライトピアノの部屋をあと一時間借りることにした. これを借りるのは今回が初めてだった. YAMAHA のピアノはこの前 (一年半ほと前) に使ったとき以来アクションの整調がされてなくて, 前のときと同じように,中低音が mp でぬけてしまったり, ダブルアクションからシングルアクションでの柔らかい打鍵への移行が全然できなくて, 結果として mf 以上の音しかちゃんと出せず, 指についてきてくれない不満の残る状態だったのだが (この状態のピアノだとハノンのおけいこのような練習, あるいは悪い状態のピアノをコンサートで弾かなくてはいけないときの対応の練習くらいしかできない), 後半に使ったアップライトピアノはすごく良い楽器で保守も行きとどいていたので,驚いてしまった. 特に,最近,ポーランドでひどいアップライトピアノに沢山触れて, アップライトピアノへの信頼感がほとんどなくなっていて, このスタジオのアップライトピアノについてもあまり期待をしていなかったので,驚きはなおさら大きかった. もっとも,保守が行きとどいている,というのは,ここのグランドピアノの方の状態を考えると, 単に良くオーバーホールされたものを買ってから時間がたっていない, というだけなのかもしれないが… こんなことなら初めからこのアップライトピアノを借りるのだったと後悔した. いずれにしても,この楽器なら,近いうちにまた弾いてみたいと思った.
このアップライトピアノは Steinmeyer という名前の楽器で,後でネット調べてみると,
Die Firma "A.Steinmeyer & Co." wurde 1922 in Berlin gegründet und existierte nur bis etwa 1927
とあった. ちなみに一字違いの Steinmayer というのもあって,こちらは現存する中国のピアノ会社の銘柄らしい. 京都は空襲にあっていないので, 古い楽器が残っていてもおかしくはないが, この Weimarer Republik の時代に5年間しか存在しなかったベルリンの Klavierfabrik で作られた,幻の楽器と, 京都で巡りあえるとは. 「また来んべ」(*)
(†)しかもこれらの議論はへんな理論武装や理論カモフラージュがなされていることが多いので,
言っている本人たちも,これが
「みんなが言っているから正しい」「偉い人が言っているから正しい」etc.
式の論法になっていることを認識すらしていない可能性さえある.
数学ではわかったつもりになって先に進んでしまう,というのは致命傷なので,
この「みんなが言っているから正しい」「偉い人が言っているから正しい」etc.
式の論法を無意識に採用してしまうことを避ける訓練を重ねざるを得ないわけだが,
そのような修行を積んでいない生臭坊主というものは,
やはり生臭坊主であるしかないのだろう.
現代のアカデミアの門にも
「(現代)数学を知らざるもの,この門をくぐるべからず」
というような自己言及の主張が書かれるべきと思う所以である.
(*)「また来んべ」というのは千葉の方言で,その意味は
「またきますね」というような感じ.西脇順三郎の詩集『近代の寓話』に含まれている,
戦時中に千葉の農家に疎開していた本を戦後になってとりに行ったときのことを題材にした詩 (詩の中に,
メタな記述として,この詩の背景を解説する数行が挿入されている) の,
最終行として使われている言葉である.
この詩は,
現実の描写とシュールレアリスティックな表現 (天使の頭がじやまになつて少しも/天国がみえない)
が交互にあらわれてそれらのイマジーュの間の往復運動の振幅が発散しかけたところで,
Debussy の曲の最後でよくあるように「また来んべ」という一言で突然流れを切ってしまう,
というあざやかな終りかたをしている.説明してしまうとちょっと uncool だが.
そもそも,我々は自分の見たいものしか見ていないかもしれなくて,. 蚕がつむぎ出す繭のような,自分自身の作りだした厚い境界皮膜が, 他の境界皮膜の内側にあって, その外側にある皮膜は,この内皮を補強しているにすぎないのかもしれない.
時折, この境界膜の存在に気付いて驚く, というのは近代人にとっての哲学的な啓示の瞬間のようなもの, と言えるだろうが, そのことに一生気付くことなく,「力強く」生きている大半の人々をどう扱えばよいのか? あるいは,初期の現象学が主張していたような,自分を無にすることで, この一番内側の皮膜を通りぬけることができる, というようなナイーヴな「理論」とはどう向かい合えばいいのか?
偽装の襲撃の舞台となったのは,この塔自身ではなくその隣にある放送管理棟で,この建物は今は歴史博物館になっている. この偽の襲撃を本当らしく見せるためにドイツの秘密国家警察は人を殺して現場に遺棄したりもしているようであるが, 全体としてはお粗末な演出で国際社会からは直ぐに偽装襲撃として非難されている.
これより8年前の日本の関東軍の演出した, いわゆる柳条溝事件も同じようなお粗末な偽装爆破事件で (ここでも襲撃をもっともらしく見せるための殺人と死体遺棄が行われている), これが偽装であることも国際社会から直ちに看破されている.時間的な関係や, 御粗末さ加減の類似性から,ひょっとするとドイツの「作戦」は日本の 「作戦」の猿真似だったのかもしれない,という気さえしてくる.
両方とも,そのお粗末さにもかかわらず進軍のきっかけとなり得たのは, 自分に徳になること (日本語で景気とか, 暮らし向きとか呼ばれているものが良くなるようなこと) なら何をやっても良いと思っている大多数の国民の破廉恥さに, 納得する口実を与えられたからであろうし, 偽装を仕掛けた側もそういう国内の反応を見越した上でのお粗末作戦であったのだろう.
この映画を大半の日本人は,現状の日本の政治/管理システムでも, 緊急の場合には正しく適用すれば勝利につながる, というメッセージとして理解するのではないかと思うが,欧米語で書かれた批評を読んでみると, 大半の評者は,この映画を,日本のクレージーなシステムに対する批判, ないしはパロディーとしての皮肉としか受けとっていないことが分る. 僕自身の視点は,かなりヨーロッパ寄りなので, 作った側は皮肉としては意図していないし (皮肉が交じっているとしてもほんの隠し味程度だろう), 日本では全く皮肉として受けとられてもいないことは理解できるにしても, つい苦笑いをしながら見てしまうことになる.
この引退のことを知ることになったのは, ネットで見つけた翻訳家/エッセイストという肩書きの日本人の人の書いた記事だったのだが, この記事には,Shizuo Kakutani も角谷静夫も出てこない.しかも, この人の「翻訳家」という肩書きに,もしかして,と思ってネットで調べてみると, この記事の文章には,2008年の The Guardian に Kira Cochane という人の書いた ''Don't mess with Michiko Kakutani'' という記事の一部が, ほとんど剽窃と言っていいような形で (日本語に訳されて) 転用されていた.二人とも同じ source から書き写したのかもしれないが.
ジャーナリズムでは,日本に限らず,出典を明らかにせずに二次資料のまたびきをしてしまう, ということはけっこう無神経に行なわれることが多いのかもしれないが, (二次資料の無神経なまたびきに関してはこんなことを書いたこともあった) この 「エッセイスト」の文章の場合には,Cochane の文章にある,複数の作家の (Michiko Kakutani を罵倒する) 発言の引用のワンセットが,ほとんどそのまま日本語に移しかえられていたのである. これで更に訳文に誤訳が交じっていたり,消化不足の流用になっていたりしていたら, この記事を書いていた日本人の名前をばらしたくなっていたかもしれない.
しかし,この「エッセイスト」, 日本人が英語を読めないのをいいことに,英文の記事の翻案で水増しした記事を,けっこう名前の知れた, しかもアメリカ系の雑誌なんかに出したりしてお金をかせいでいるのだろうか.
ちなみに,この Kira Cochane という人の文章の方には,Shizuo Kakutani の名前こそ出てこなかったが,''her father was a mathematician'' という一文があった.
この映画の英語のタイトルは "Radiance". このタイトルからの連想で西脇順三郎の "百舌鳥の舌にも永遠のひかり" という詩句を思い出して, この文句が頭の中を離れなくなってしまった. 晩年の詩のどれかにあったのだと思うのだが,うまくみつからない.
「永遠のひかり」は, ラテン語の lux aeterna で,「光」はむしろ,この l の音で始まる light とか luminance とかの系列の単語で, radiance は光自身より光の明るさや光の筋を表わす言葉だろう. 志賀浩二の『無限からの光芒』の「光芒」は radiance と訳せるかもしれない. --- radiance from the infinitude --- ただし,映画の題の方の『光』は 「光を失なう」という日本語の成句などにある「視力」の意味の含みもあったのかもしれないので, これをうまく英語のタイトルに置き換えるのはいずれにしても難しかったのかもしれない.
考えることの達人だった Erdős Paul (ハンガリーでは日本と同じに苗字名前の 順に人名を言います --- ちなみに,ここでは英語の wikipedia をリンクしましたが,日本語の wikipedia ページはほぼこの英語版の翻訳になっています.おまけに, この日本語版は笑える誤訳がいくつもあるので大変楽しめるものになっています) の逸話に, Erdős が橋の上に立って考えていた.警官が不審に思って 「何をしているんですか?」と尋ねたら Erdős が "I'm thinking." と答えた, というのがあります.確か第二次世界大戦前のロンドンでの出来事だったと思います. これは数学者向けのジョークと言えると思いますが,一般の人の思っている 「考える」は数学者のスタンダードでの (深く) 考えるということとは全く別の意味になる, ということでしょう.一方,数学者でない数学者のパートナーの側からのジョークというの もあって,これは, この間, ポーランド人の数学者の (数学者ではない) 奥さんがワインの試飲会 (といってもかなり飲んだり食べたりする会) の折, 皆がもういいかげん酔っぱらってきたときに言っていたものですが, 数学者とそのパートナー (数学者は男性の方が多いですが, どちらが男性でも成立するジョークです) がベッドに横になっていて 「同じことを考えている?」「うん」「...」「...」 「じゃああんたの証明を言ってみて」というのがありました. もちろん二人とも数学者だったら,ここで議論 (これも一般の人には通じにくい概念かもしれません) が始まる,という ジョークではない展開になるわけでしょう.
というわけで,「普段の数学との付き合い方」は常に考えていること, ということになると思います.これはかなり反社会的な行動で, 本格的にやろうとすると回りの人にも迷惑をかけることになる行動でもありますが,このことの帰結として,車は運転しない, とか,合法非合法は問わず麻薬はジョイントでは服用しない, といった生活パターンも決まってきます.数学者の車の運転は, 運転中に考えはじめてしまうことがあるので,大変危険です. 麻薬 (酒など) を数学者でない人とジョイントで飲むと思考を不自然な瞬間に中断しなくてはいけなくなるので, これは (数学の) 思考にとって危険です. また麻薬の脳におよぼす長期的な影響というのも無視できません.
しかし逆に休みなく考えていることは,必ずしも効率的ではなくて, 何らかの気分転換が必要になることも多くあります. 何かの気分転換があった直後にそれまで考えていた部品が魔法のように組み合さって問題があっけなく解けてしまう, という体験は多くの数学がしているもののようで, ポアンカレの自伝を始め (ポアンカレは馬車を降りた瞬間に問題が解けた自分自身の体験を語っています), 多くの人が触れているものです. よくあるパターンには, 考えてどうしても分らなくて,眠ることにすると夢の中で問題が解けたり, 朝に起きた瞬間に分ったりするというのもあります. また,私の場合は,日本人の数学者と一緒に酒を飲むことはほとんどないのですが (特に日本の場合,年功序列のようなもののために若い数学者とうまく話をすることができないので), 国際学会の折などに,研究テーマのある程度近い (あるいは全く分野の違う, いずれにしても様々な世代の) 数学者と一緒に酒を飲んで, 色々なテーマの雑談とディスカッションの間を行き来するような会話をすることはあります. これは目がさめたときに問題が解ける, というときのようなドラマチックな展開を伴なうことはまずないのですが, 考えがつまったときの気分転換としては有効なことが多いように思えます.
[この項はまだ書きかけです.]
しかしよく聞いてみると,これをけしからんと言う人は, 数学は拷問のようなものだ,と思っていることが多いようです.多分上の2つの質問も, (ドイツ語が分れば) "Mathe macht glücklich" をけしからんと思う種類の人の発想なのではないかと思います.
「ハマる」というのが addiction の状態を指す言葉だとすると,これは前の言い方でいうと (狭義の意味での) 数学の研究の局面を記述する言葉ではないように思えます. 「普通」の人から見るとありえない精神集中が必要なことは確かですが,これは, addicted な状況とは無縁なものに思えます.
ただし, 人間も含めて動物のすべての行動のモティヴェイションは (哲学的にも生物学的にも) addiction と同一視できるようなものでしかないのかもしれない,という気もしています. 生きていたい,死にたくない,と思うこと自身が生への addiction にすぎないのかもしれない,というのはよく頭をよぎる考えです.
一方, 「数学の魅力とは」という質問については,もちろん色々な答を言うことができます. なぜ数学が好きになったのか (3) でも述べるように, 考えに考えぬいてもわからなかったことがあったとして, それが何かのきっかけで, それまでにこの問題の解決にもけて組み立てていた思考の部品のいくつかが魔法のように組み合さって問題があっけなく解けてしまう, という体験をすることがあるのですが,主観的には,このようなときには, 急に視界が開けてすべてが明白に見渡せるように感じます. このとき感じる快感は,上で言ったこととは矛盾するけれど, 麻薬的と表現することもできるかもしれません.ただし,このような瞬間は, ただ待っているだけで来るわけではなくて, 少なくとも理詰めでつめられるところは全部詰めてしまったような状況を作ることが必要で, しかも逆にそのような状況を作ったとしても, この啓示の瞬間が来るという保証はなくて, ただ考えにつまるという状況に行きついてしまうことも少なくありません.
上で言ったような数学の「魅力」の感じかたは,多くの数学者に共通のもののようです. 次の文章は志村五郎先生 (以下敬称略) の『鳥のように』の中にあるものです:
数学者にもいろいろあって、純然たる「パズル解き」型の人もかなりいる。 しかし、多くの数学者の心を惹きつけているのは、この未知の世界へのあこがれと挑戦、 つぎにどうなっていくかわからないというスリルにみちた日々の体験、 そして徐々に姿を現わして来る秩序の美しさにある。
ここで志村が『純然たる「パズル解き」型』と言っているのは, 私が なぜ数学が好きになったのか で 「狭義の数学」と呼んでいるものに対応するものと考えていいでしょう. また 「秩序の美しさ」といっている美しさはもちろん美学的な美しさでもあるのでしょうが, 抽象的な,世界の理解の仕方の表現になっていることの美しさ, ということでもあるのだと思います. この志村五郎の言葉は私にはとてもよく分るのですが, 一方彼の研究は僕のやっている研究とはかなり重心は異なっていて, ものの見方もかなり違うと言っていいと思います. 数学の内容に関しては前に彼が文庫本で書いたことについて,つい 苦言 を 一つならず 書いてしまったことがありました.
そういう違いにもかかわらず,数学者どうしが十分互いに共感できる, この数学の魅力は,数学の外にいる人 (この人たちの多くは, 生れてから今まで数学の魅力が認識できないできた人たちなわけでしょう) にはなかなかうまく説明ができないことなのかもしれなくて,志村五郎が上の文章の題としている, 勝事空自知 (勝事は空しく自らを知る) という感じなのかもしれません.
ところで,ここで「考える」とわざと目的語を言わずに言っているのは, ヨーロッパの科学文化の伝統の文脈の中で言っているつもりです.パスカルなら目的語は (キリスト教の意味での)「神」ということになるのでしょうが, これは言葉をかえれば,「宇宙 (universe) を理解する」ために考える,と言うことができるでしょう. この「宇宙を理解するために考える」という行為によって 「全てが理解できている」という状態に至ることは不可能だということが, 20世紀に得られた知見の一つであるわけですが (不完全性定理など), このことは言葉をかえれば,我々はどこまでも考えを進めることができる, ということでもあるわけです.
[この項はまだ書きかけです.]
このホールにあるピアノは,それまで聞いたことのなかった Seiler という銘のフルグランドピアノで, フレームの刻印から 1920〜1930年代のものらしかった. 最近替えたらしい絃が何本か狂いまくっているのが残念なのだが,ピアノ自身はとても良い楽器で, 東工大のデジタルホールの Bechstein をちょっと思いださせる.中音部で mp から f にむかって歌い込むと,鼻にかかったような甘い音色を引き出すことができる.
インターネットで調べてみると,この Seiler というピアノメーカーは戦前, 低シレジアの Legnica (ドイツ語では Liegnitz) にあったメーカーで, 一時期は世界的に大変高い評価を受けていたらしい.大戦終結後は Seiler 社長をはじめドイツ人のスタッフは西ヨーロッパに避難して最初にコペンハーゲン, その後に西ドイツで工場を持ち,会社は2008年に韓国のピアノ会社 Samick (삼익악기(三益樂器)) に吸収されたということである.
実は,インターネットで調べていて, この Legnica という場所は, 数学者としての僕にとっても特別な場所であることに気がついた.ここは, Kronecker の生れ育った (そして博士取得後ビジネスで成功して財をなした) 街だった. 今,ポーランド数学会のシレジア分科会と, ポーランド学芸アカデミーのシレジア分科会で講演を依頼されていて, どちらの講演でも,Kronecker と Cantor の確執から話を始めて, 「数学の自由性」について議論してみたいと思っているところなのだ. もちろん数学会の方では, 多少数学的な話 (前にも別のところで議論したことのあるゲーデルの加速定理にからめた話) もすることになる予定である. この2つの講演では,どちらかというと Cantor の側に立った議論になるのだが, Kronecker を全否定するわけでもない. うまくこのシレジア出身の数学者の視点をも含めた総合的な数学像について話ができればよいと思っているところなのである.
[付記 19.09.23(月13:28(JST))] ここで言っている「ゲーデルの加速定理にからめた話」はその後,
[1] 渕野 昌, 数学と集合論 --- ゲーデルの加速定理の視点からの考察}, 科学基礎論研究,Vol.46, No.1 (2018), 33--47.
に纒めた.これを更に拡張した英語版を準備しているところである.「一言で述べよ」式の解答しか受けつけられない大多数の人たちに何か本質的なことを説明できるのか, ということについて,僕は否定的な経験を積みすぎてしまっているような気がする. だから, 「ベストセラー」というようなカテゴリーの文章を書いている作家というのは, とても恐しいような気がするし, この恐しさが僕の究極の攻撃性を引きだしてしまいそうなことに対する恐しさもある. しかし,その反面,この「ベストセラー作家」という現象には, ひどく好奇心をそそられもする,… というのがこのインタヴューを受けることを承諾してしまったことの背景である.
***
リストの最初の2つの質問は,この post のタイトルにある 「なぜ数学が好きになったのか」と,「なぜ数学の道を選ばれたのか」です. 最初の文に敬語が用いられていなくて二番目の文に敬語が用いられているのは不気味ですが, それについては目をつぶることにすると,これは, 理論物理学や,天文学や,哲学や, 経済学や,芸術や文学などがある中でなぜ (よりによって) 数学が好きになって, それを職業として選んだのか, というような意味の質問ではないかと思います.
狭義の「数学」に対しては, このような質問ができるかもしれなくて, 「他のことが何もできなかったので数学を選んだのです」というような, 「職人 (モダンな日本語では 「プロフェッショナル」とも言う) のモラル」 の大好きな日本人を喜ばせそうな答を返せる人もいるかもしれません.
しかし, 私にとっての数学は, むしろ広義の「数学」で,それは 「(理知的に) 考えるときの正しい(抽象的な) 方法」を指す言葉にすぎない. だから,私が自分を数学者と名乗ることは,理知的に考えぬくことを決意した, ということの表明にすぎなくて,「道を選ぶ」ということで言えば, むしろ何かの道を選んで, その道に特化した''専門家'' とか ''職人'' とか (日本語で言うところの) ''プロフェッショナル'' になってしまうことを拒否したのだ,というのが私自身の認識なのです.
実際, (上の意味での広義の) 数学が,その抽象性から分野の壁を楽々と超えてしまう, という例を我々は沢山知っています.英語で polymath ドイツ語で Universalgenie などと呼ばれる広範囲の学問領域で重要な貢献をした人は,ほとんど全員数学者です: たとえば,アルキメデス, ライプニッツ,ガウス,フォンノイマンなどの例を思い出してみてください.
抽象性は,「職人」の文化では否定的にとられることが多い概念ですが, これは個別の現象の裏にある共通の本質をとらえる,ということです. たとえば,時代が早すぎて,共通の本質を語るための数学の創造には至れなかったけれど, 寺田寅彦が線香花火や割れ目や縞馬の模様の背景に見た共通の何かや, こちらの方は,数学の手立てを持っていたために, 定式化することのできた,テューリングによる, ある種のコンピュータネットワークと蝶の羽の上の紋様の背後にある共通の概念など, 人為的な「分野」の垣根は抽象的な数学 (とその応用) にとって意味を持たないことが多いのです.
一方,ここで「広義の数学」と呼んでいる種類の数学には,上で言った 「個別の現象」を出発点とせずに, 抽象のための抽象としての抽象概念を研究してゆく,という姿勢もあり, これが,和算のような遊芸としての数学と混同されることもあるのではないかと思います. しかし,この「抽象のための抽象」は,それが「正しい」方向を向いているときには, その応用ないし意味付けが予定調和的に後からついてくる,という現象が非常に頻繁に起ります.
歴史上の例をいくつか見てみると, 19世紀後半に抽象的線型代数の理論が研究されていたときには, これは「抽象のための抽象」と看倣されていたのではないかと思います.しかし, 現在では,線型代数は代数や幾何, 解析学など広範囲な数学理論を統一的に見るために不可欠な枠組を供するものであることが知られています. 日本語で書かれた線型代数の教科書は, 線型代数のこのような位置付けを初学者に説明する努力をしていないものが多いので, 学部の1年で習う線型代数の講義を普通に受けただけでは, そのことの理解に至らないかもしれないですが, アメリカの教科書のいくつには, 線型代数の数学や数学の応用全般に対する役割について, 初学者に対する丁寧な説明がされているものもあります.
また,これは上に述べた近代的な線型代数とも関連するのですが, クーラントとヒルベルトの解析教程が書かれたときには,この本の抽象的な記述は, 多くの物理学者にとって,必要以上に抽象的なものに見えたかもしれません. しかし,この少し後に量子力学が導入されたときに必要となったのは, まさにこの解析教程で展開された数学でした.
上で,「正しい」方向を向いている「抽象のための抽象化」と言いましたが, この「正しい」は最初から数学者の直観によって見極められている場合もあるのですが, 後になって,色々やってみたうちの一つが正しいことが分った, という流れをとる場合もあるし, 最初は正しくないとして破棄されたものがずっと後になって (この場合の「ずっと後」は数十年の場合もあるし, 数世紀の場合もあります),実は別の意味で正しいことがわかった, という展開になることもあります.だから,色々試行錯誤してみるということも必要で, その意味では, 「遊芸の数学」と上で否定的に表現した数学研究のスタンスも, 実は,大きな数学の流れの中では重要な役割をになっているのだろうと思います.
日本では,「(理知的に) 考えるときの正しい方法」としての数学を行なっている, というような発言には, 「なんと尊大なことを言うか」というような拒絶反応が帰ってきそうな気もします. 今ちょうどヨーロッパに帰ってきているところなので,ここから振り返って見ると, そういうような反応の帰ってくる可能性のある日本,というのがひどく疎ましく感じられます.
そうは言っても,もちろん Universalgenie になる度量のない人が, それを目指すことが必ずしも建設的なことではないかもしれなくて, 少なくとも個人の幸せというような観点からは, 職人の完成度を目指す方がずっと健全なことかもしれないので,この 「なんと尊大なことを言うか」という反応も,全くの空回りではないのかもしれません. しかし,それを言うなら,そもそも数学者の「道」(?) を選ぶことがすでに, (日本での?)個人の幸せとは相容れないものになっているわけなので, そう考えてみると, 「なんと尊大なことを言うか」は,少なくとも数学者 (を自認している人) に対しては御門違いのコメントでしかない, と言っていいのではないでしょうか.
かつて岡潔は, 「野原の中で咲いているすみれは自分が野原のどこで咲いているかを知っている必要はない」, というようなことをどこかに書いたことがあったと思います. 今手元に文献がなくて記憶で書いているので, 文言は正確ではないかもしれませんが. これは, 「数学なんか研究して何になるのか」というような質問をしつこくされて, 嫌気がさして言った言葉だったのかもしれませんが,とりようによっては, すみれの分際で自分が野原のどこに咲いているかを知ろうとするのは尊大なことだ, と言っているようにも読めます. これは和算的人生観とは言えるかもしれませんが, 西洋数学の伝統に連なる数学を研究しているものとしては (ちなみに私の学問的祖先には, オイラーやライプニッツや彼等の前後の世代のフランスの数学者たち, カントやフィヒテなどのドイツの哲学者などが含まれています (詳しくは ここをご覧ください)), たとえすみれにすぎなかったとしても, 自分が野原のどこに咲いているかを見極めつつ可憐な花を咲かせたいと思うのです. この宇宙の夢を見ているすみれの思考が, 宇宙全体 (の認識) を根底から覆してしまうような胡蝶効果 (butterfly effect) を起こさないという保証だってないわけですから.
[この項はまだ書きかけです.]
Gunnar Asplund (1885--1940) 設計の 1928年開設の図書館で, Wikipedia によると, この建物に隣接する拡張の計画のコンペティションで日本にもゆかりのある(らしい) Heike Hanada というポツダムにオフィスを持っている建築家が優勝したということである.
David は 「ナチの建築もそうだけど, この時代の建築は威圧的でどうもね」などとも言っていたが, もしこの街に住んでいたとしたら,この図書館に毎日通って一生を終える, という人生を送るのもいいかな,と一瞬思ったのだった.
「宇宙図書館」というのは universal library の意図的な誤訳だが, この記事を書いてからしばらくして, ユーミンの 『宇宙図書館』がまさにこの Asplund の図書館からインスパイアされたものだったらしい, という記事をインターネットで見つけてびっくりした.
しかし,驚いたのは,その講演の直後に David Fremlin 先生が演壇に上がってきて, 本 (後で手漉き紙のつつみを開けてみたら,彼の叔母さんでミステリー作家だった Celia Fremlin 1914-2009 の代表作のペーパーバックだった) をプレゼントしてくれたことだった. しかも,「すばらしい講演もそうだが, 先日のピアノのコンサートに感謝して」ということだったので更に面くらってしまった.
確かにこの講演のあった日より前,夕食の後, 学会会場の食堂としても使われている, 昔ここを所有していた貴族のお城の中の一室に置いてあったアップライトピアノを遊び弾きして, 弾きおわって気がついたら結構の人数の人が演奏を聞いていたことが分ってびっくりしたことが何回かあった. しかし,これはかなりいいかげんな演奏で, そのうちの1回は晩餐のワインを飲んでからの演奏だったので, いいかげん以上 (以下?) のものだった . そのうえ,このピアノはメゾフォルテしか出ないような,どうしようもない楽器で (''Europa'' という聞いたことのない銘柄のアップライトピアノだった. 中は見ていないがタッチが他のピアノと全く違っていたので独自のメカニックが使われているのかもしれない. しかし何しろ表現の可能性が限定されすぎていて, クラシック音楽を弾くための楽器とは言えない代物だった), そのことだけからでも,ちゃんとした演奏をすることは不可能に思えたし, 褒めるのなら,もっと良い楽器で, (しらふで) 気持よく細かいニュアンスまで演奏できたときにしてほしい,というのが本音だった.


それにもかかわらず,このどうしようもないピアノを何度も弾いてしまったのは, ピアノが置かれていたのが, ショパンがまだポーランドで天才少年だったころに請われてピアノを弾いたであろう貴族の館と同じ時代の, やはり貴族の所有していた多分同じような間取りの建物で, だから, 幼いショパンがホームコンサートなどでピアノを弾いたときのアクスティックスもここと同じようなものだったのではないか, という興味からだった.それで, 指になじんでいなかったのでエコセーズなどショパンがまだポーランドにいた時期のピアノ曲こそあえて弾かなかったものの, 普段は人前では絶対に弾かない Preludes のうちのいくつかやワルツなども弾いてみた.
僕の講演があったのは学会の最終日で,この日は, ピアノがあまりにひどいのでもう弾くのはやめようと思っていたのだが, 本までもらってしまったので,夕食の後にもう一度このピアノの弾きおさめをした. 疲れていたので,早々にやめてしまったが, 弾いたのはムズィカ・カヤダの第1集とショパンを何曲か (このときにサービスで e-minor prelude --- James Rhodes が「こんな曲があなたも弾けたら素晴しいでしょう?」と言ってこれを弾いている YouTube の post がある --- や「雨だれ」も弾いたんじゃなかったかと思う),それにラベルの死せる王女へのパヴァーヌ. さそうあきらの『神童』を読んで以来,この楽器を弾くのはこれが最後, というときにパヴァーヌを弾くというのが僕の儀式のようなものになってしまっている. スタちゃんには及びもつかないくそピアノでも, 弾くのはこれが最後というときには,ちょっとは名残り惜しい気もする.
● 上で数学者の名前に 「先生」をつけたが, これは,ここで触れた人たちが, この敬称をつけるのが自然な高名な数学者たちだからでもあるが, 実際に彼等が全員僕より年齢が上の人たちだったからでもある. 最近,出席した学会で参加者の中で僕が最年長であることが判明して, ちょっと居心地の悪い思いをする, ということが時々起るようになっているのだが,そのような学会に比べると, この学会の参加者の平均年齢はかなり高かった,と言える. ここで挙げた人たちのうち,残念ながら Sabine は研究からリタイアしてしまったが, 他の人たちは皆,今も精力的に研究を続けている. 僕より年長の数学者でまだ元気に研究を続けている人が沢山いるのを見ると勇気がわく.
Frühling, Sommer, und Herbst genoß der glückliche Dichter;
Vor dem Winter hat ihn endlich der Hügel geschützt.
春,夏,秋を,この幸福な詩人は満喫したが
遂に来た冬から,彼を墓陵が守ってくれているのだ.
数理論理学は, 19世紀後半以降,数学の (数学的,哲学的 etc.) 基礎付けとの関係で発展してきた分野であり, 日本語での「数学基礎論」という分野の名称 (?) もそのことを示唆するものであろう. ただし,日本語で「数学基礎論」と言ったときに, その示唆する研究分野のイメージは, 英語で ''Logic'' ないし ''Mathematical Logic'' と言ったときに起想するそれとはかなり違ったニュアンスを持ったものになっているようにも思える (ちなみに私は自分の研究を,この ''Logic'' ないし ''Mathematical Logic'' に属すものと思っているので, 「ご専門の数学基礎論では …」などと言われことがあると,数学と縁のない人から 「数学をやっているのなら計算がお得意でしょう」というようなコメントを頂いたときと同じような異和感を感じる).
しかし,近年,数理論理学は,計算機科学との関連のみにおいて 論じられたり講義されたりすることが多くなっており, そのような導入のされ方が採用されることで,数理論理学の旧来の数学との関連や, 最先端の数学としての数学の他の分野との共生 (symbiosis) の可能性が見えきにくくなっているように思える. 本書での数理論理学の扱いが,そのような 欠落を補うための役割を少しでも果してくれることを願うものである.
Welch ein Grab ist hier, das alle Götter mit Leben
Schön bepflanzt und geziert?, Es ist Anakreons Ruh.
Frühling, Sommer, und Herbst genoß der glückliche Dichter;
Vor dem Winter hat ihn endlich der Hügel geschützt.
(Johann Wolfgang von Goethe)
日本は,左利きの差別の強い国だと思うが,東アジアの中ということでは, この差別は比較的穏便なものである,と言えるかもしれない.しかも, 左利きの日本の社会でのステータスは近年ずいぶん変ってきているかもしれない.
大学に務めていると試験の監督をしなくてはいけないことが少なくないのだが, これは左利きの統計をとる格好の機会である. そのような機会に左手で文字を書いている人を観察してみている経験から言えることの1つに, 近年左ききの若い女性がとても増えている,ということがある. これは,左利きのアカデミックの女性が増えている, ということなのかもしれないが, 最近店舗のカウンターで仕事をしている日本人の女性で左ききの人に何人か遭遇したりもしたので, 特に大学で理科系の勉強をしている女性だけに限った現象でもなさそうである.
僕の世代では, 左ききは子供のときに矯正されることが多かった. 特に女性は,例の 「お嫁に行けなくなる」という普遍的(?)判断によって, 厳しく矯正されることが多かったのではないだろうか. それが最近変ってきた,ということなら,これはどういう変化を意味するのだろうか?
日本はヨーロッパやアメリカに比べると,社会の (社会の仕組自身や,その文化で固定されたものや, その中にいる人の) 左利きに対する差別がかなり大きいと言えるように思うが, アメリカ合州国については,何十年ぶりかで右利きの大統領の政権が確立したことから, これから,アメリカでのこの差別のゆるやかさに変化が出てくるかもしれない.
少なくとも,ユニバーサルデザインの観点からは, 日本は,意識的に右利き用にデザインされたもので溢れている. 日本製のバターナイフや急須, 電気アイロンなど,すべて右利き用とするためのアンティシンメトリーが加えられている.
左利き用のはさみ, 包丁,ワインのコルクぬきなどを, 少し余計にお金をはらうと買うこともできるのだが, 日頃右利き用の製品を無理して使うことに慣れていると, 逆に左利き用の製品を自然に使おうと思ったときには特別なトレーニングが必要になる. (バターナイフについてはスウェーデン製のシンメトリカルなものを買ってきて使っている)
こういった「左利き用製品」に対する揶揄として 「左利き用のカップ」というジョークがある (日本語ではコップと言うとガラス製で持ち手のないものを指し, カップというと持ち手のあるものを指すことに注意). しかし,僕が家で使っているマグは本当に右利き用である. これは日本の製品ではなく,韓国の Starbacks cafe でかつて売っていたマグで, 훈민정음 (訓民正音) のテキストが側面に書いてある.

特に興味深かったのは,第二次世界大戦/大平洋戦争の時代の広告だった. 日本の「欲しがりません勝つまでは」の余裕のなさとはまったく対照的な状況を示唆する広告ではあるが, ニューヨークが総力戦としての戦争を真剣にサポートしていたことがうかがえるものだった. 冷戦時代の興味深い広告もあったが,この話はここでは省略する.
下の写真はニューヨーク州出の"ヒーローズ"をたたえるポスターと, 「結核は勝利を遅らせる」というレントゲン検査をうながすポスター. ポスターでの敵の名前は,ドイツが NAZIS と政党の名前で呼ばれているのに対し, 日本は JAPS, NIPS と国全体,総国民を指す蔑称が使われている. これは,戦時中, アメリカ (やカナダ) で日系人が国籍が日本かどうかにかかわらず concentration camps に送られたのに対し, ドイツ系アメリカ人がそのような扱いを受けなかったという違いにも対応していると言えるだろう. ただし,ドイツ系人も敵性国人として良い扱いは受けなかったようで, たとえば,wikipedia によるとトランプ大統領の家は, 戦争中には自分たちがドイツの血筋をひくことをひたかくしに隠したということである.
ちなみに, 今日 (17.02.25) ネットにあがった ARD のコメントに "..., können wir uns hoffentlich wieder wichtigeren Themen zuwenden. Trumps Russland-Verbindungen zum Beispiel, oder seinen zahllosen Interessenkonflikten, oder seinem angespannten Verhältnis zur Wahrheit. Denn eines muss dem Weißen Haus klar sein: Kritischer Journalismus funktioniert auch ohne Kooperation." とあったが, "sein angespanntes Verhältnis zur Wahrheit" に関しては,このドイツのルーツをひた隠しにした,というトランプ家の歴史は, その大きな背景の1つになっているのではないかという気がする.


その週末に Rothmaler 氏の家に招待された.お客さんが来るときの料理は彼の担当ということで, 美味な料理とワイン apple cider (ベルリンの Apfelschorle のような軽く発酵した飲み物) をいただいた. 彼の家には, Elton John が昔弾いたことがある,といういわくつきの白いヤマハがあって, 譜面台に乗っていたアンナ=マグダレーナの音楽帳の Henle 版の楽譜を遊びびきしてみた.この曲集の中には,François Couperin の 6me Ordre の Les Bergeries が含まれている,というのがずっと気になっていたことだった. これは,Couperin の Bach に与えた影響を評価するときの重要な資料の1つと言えるだろう. 実際 Henle 判の譜面にもこの曲が含まれていた. 弾いてみると,譜面づらが原曲と全く違っていて (たとえば ABACA の A の部分の伴奏は Couperin 特有の "リュート書法" (style luthé) ではなく一声の線として書かれていた. この "リュート書法" は Bach 自身 Partiten の中の遅い曲などでは取り入れている書法なので, ここでそれが採用されていないのは,この曲が Bach に伝わったときにすでにこの形になっていたのでなければ,Bach 自身の初心者への配慮からの編曲だろう) 修飾音もかなり違っていた. Henle 版は原典版と称しているので, 多分 Bach の書法のある程度正確な再現になっているのだと思うのだが, この曲がどういう経緯で Bach に伝わったのかは非常に興味があるところだ.
原曲とすごく違う気がして,びっくりしながら弾いていたのだが,後で帰ってから楽譜を比較してみると, 逆に,(この曲が,何回かの写譜を経由して Bach に伝わったのだとすると,それにしては) 原曲が非常に忠実に保たれている, とも言えるように思えてきた.
 Last modified: Wed Nov 26 01:55:39 JST 2025
Last modified: Wed Nov 26 01:55:39 JST 2025